Double Tank multimode problem

Double Tank multimode problem
State dimension:	1
Differential states:	2
Discrete control functions:	3
Interior point equalities:	2

This site describes a Double tank problem variant with three binary controls instead of only one control.

Mathematical formulation

The mixed-integer optimal control problem is given by

$\begin{array}{llll} \displaystyle \min_{x,w} & \displaystyle \int_{0}^{T} & k_1(x_2-k_2)^2 \; \text{d}t\\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = \sum\limits_{i=1}^{3} c_{i}\; w_i,-\sqrt{x_1}, \\[1.5ex] & \dot{x}_2 & = \sqrt{x_1}-\sqrt{x_2}, \\[1.5ex] & x(0) & = (2,2)^T, \\[1.5ex] & 1 & = \sum\limits_{i=1}^{3}w_i(t), \\ & w_i(t) &\in \{0, 1\}, \quad i=1\ldots 3. \end{array}$

Parameters

These fixed values are used within the model.

$T=10, c_1=1, c_2=0.5, c_3=2, k_1=2, k_2=3.$

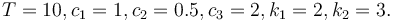
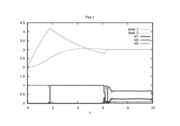
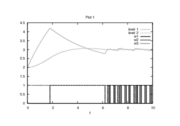
Reference Solutions

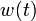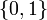If the problem is relaxed, i.e., we demand that $w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$, the optimal solution can be determined by means of direct optimal control.

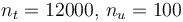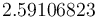The optimal objective value of the relaxed problem with $n_t=12000, \, n_u=100$ is $2.59106823$. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is $2.59121008$.

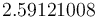• Reference solution plots
• 

  Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and $n_t=12000, \, n_u=100$.

• 

  Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and $n_t=12000, \, n_u=100$. The relaxed controls were approximated by Combinatorial Integral Approximation.

Source Code

Model description is available in

• AMPL code at Double Tank multimode problem (AMPL)