Isomerization of Alpha-Pinene problem

Isomerization of Alpha-Pinene problem
Algebraic states:	5
Continuous control values:	5
Path constraints:	5

The Isomerization of Alpha-Pinene problem tries to determine "reaction coefficients in the thermal isometrization of 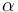$\alpha$-Pinene." (Cite and problem taken from the COPS library)

Mathematical formulation

The problem is given by

$\begin{array}{llcl} \displaystyle \min_{\theta} &\sum\limits_{j=1}^{8} &&||y(\tau_j; \theta) - z_j||^2 \\[1.5ex] \mbox{s.t.} & \dot{y}_1 & = & -(\theta_1 + \theta_2) y_1, \\ & \dot{y}_2 & = & \theta_1 y_1, \\ & \dot{y}_3 & = & \theta_2 y_1 - (\theta_3 + \theta_4) y_3 + \theta_5 y_5, \\ & \dot{y}_4 & = & \theta_3 y_3, \\ & \dot{y}_5 & = & \theta_4 y_3 - \theta_5 y_5, \\ & \theta_i & \geq & 0 \quad i = 1,...,5. \end{array}$

Parameters

The values 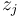$z_j$ are measurements for the concentration for 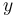$y$ at time points $\tau_1, ..., \tau_8$ and initial conditions are known.

Source Code

Model descriptions are available in

• AMPL/TACO code at Isomerization of Alpha-Pinene problem (TACO)