Marine population dynamics problem
From mintOC
| Marine population dynamics problem | |
|---|---|
| Algebraic states: |
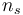 |
| Continuous control values: |
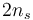 |
| Path constraints: |
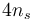 |
The Marine population dynamics problem estimates growth and mortality rates of a marine species at each stage (for example ages or development stage) given the population as a function of time.( Problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{g, m} & \sum\limits_{j=1}^{n_s} &&||y(\tau_j; g, m) - z_j||^2 \\[1.5ex]
\mbox{s.t.}
& \dot{y}_j & = & g_{j-1} y_{j-1} - (m_j + g_j) y_j \qquad \forall j \in 1, ..., n_s,\\
& g_j, m_j &\in& [0,1].
\end{array}](https://mintoc.de/images/math/a/a/5/aa54649329dc309f2284e509e6e5abc1.png)
where 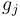 and
and 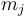 are the growth and mortality rates at stage
are the growth and mortality rates at stage 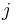 respectively and the initial conditions are unknown.
The error between computed and observed data is minimized.
respectively and the initial conditions are unknown.
The error between computed and observed data is minimized.
Parameters
There are 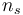 stages and
stages and 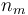 timepoints at which the error is minimized.
timepoints at which the error is minimized.
Source Code
Model descriptions are available in