Difference between revisions of "Goddart's rocket problem"
From mintOC
FelixMueller (Talk | contribs) (→Mathematical formulation) |
FelixMueller (Talk | contribs) (→Mathematical formulation) |
||
| (10 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Dimensions | ||
| + | |nd = 1 | ||
| + | |nx = 3 | ||
| + | |nu = 1 | ||
| + | |nc = 1 | ||
| + | |nre = 4 | ||
| + | }} | ||
| + | |||
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude. | In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude. | ||
| − | + | ||
== Variables == | == Variables == | ||
| − | The state variables <math>r,v,m</math> describe the altitude(radius), speed and mass. | + | The state variables <math>r,v,m</math> describe the altitude(radius), speed and mass respectively. |
The drag is given by | The drag is given by | ||
| Line 18: | Line 26: | ||
\begin{array}{llcll} | \begin{array}{llcll} | ||
\displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex] | \displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex] | ||
| − | \mbox{s.t.} & \dot{r} | + | \mbox{s.t.} & \dot{r} & = & v, \\ |
| − | & \dot{v} | + | & \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex] |
| − | & \dot{m} | + | & \dot{m} & = & -b T_{max} u, \\ |
| − | & u( | + | & u(t) &\in& [0,1] \\ |
& r(0) &=& r_0, \\ | & r(0) &=& r_0, \\ | ||
& v(0) &=& v_0, \\ | & v(0) &=& v_0, \\ | ||
& m(0) &=& m_0, \\ | & m(0) &=& m_0, \\ | ||
& r(T) &=& r_T, \\ | & r(T) &=& r_T, \\ | ||
| − | & D(r | + | & D(r,v)&\le& C \\ |
| − | & T free | + | & T \, free |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 61: | Line 69: | ||
Image:Goddartmass.png| Mass m over time. | Image:Goddartmass.png| Mass m over time. | ||
</gallery> | </gallery> | ||
| + | |||
| + | == Source Code == | ||
| + | Model descriptions are available in: | ||
| + | |||
| + | * [[:Category: Bocop | Bocop code]] at [[Goddart's rocket problem (Bocop)]] | ||
| + | * [[:Category: AMPL/TACO | AMPL/TACO code]] at [[Goddart's rocket problem (TACO)]] | ||
== References == | == References == | ||
The Problem can be found in the [http://bocop.org/ BOCOP User Guide]. | The Problem can be found in the [http://bocop.org/ BOCOP User Guide]. | ||
| + | |||
| + | [[Category:MIOCP]] | ||
| + | [[Category:Aeronautics]] | ||
| + | [[Category:Minimum energy]] | ||
| + | [[Category:ODE model]] | ||
| + | [[Category:Path-constrained arcs]] | ||
| + | [[Category:Sensitivity-seeking arcs]] | ||
Latest revision as of 18:08, 22 February 2016
| Goddart's rocket problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Continuous control functions: | 1 |
| Path constraints: | 1 |
| Interior point equalities: | 4 |
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.
Contents
[hide]Variables
The state variables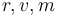 
describe the altitude(radius), speed and mass respectively.
The drag is given by
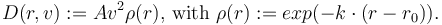
Mathematical formulation
![\begin{array}{llcll}
\displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex]
\mbox{s.t.} & \dot{r} & = & v, \\
& \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex]
& \dot{m} & = & -b T_{max} u, \\
& u(t) &\in& [0,1] \\
& r(0) &=& r_0, \\
& v(0) &=& v_0, \\
& m(0) &=& m_0, \\
& r(T) &=& r_T, \\
& D(r,v)&\le& C \\
& T \, free
\end{array}](https://mintoc.de/images/math/1/5/1/1510d912f548b873254257dbd8da014e.png)
Parameters
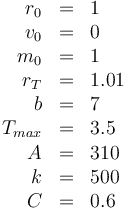
Reference Solution
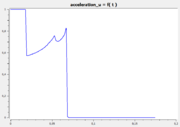
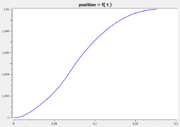
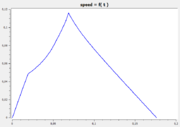
The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389.
- Reference solution plots
Control u over time.
Position r over time.
Speed v over time.
Mass m over time.
Source Code
Model descriptions are available in:
References
The Problem can be found in the BOCOP User Guide.
