Difference between revisions of "Goddart's rocket problem"
From mintOC
FelixMueller (Talk | contribs) (→Mathematical formulation) |
|||
| (15 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Dimensions | ||
| + | |nd = 1 | ||
| + | |nx = 3 | ||
| + | |nu = 1 | ||
| + | |nc = 1 | ||
| + | |nre = 4 | ||
| + | }} | ||
| + | |||
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude. | In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude. | ||
| − | + | ||
== Variables == | == Variables == | ||
| − | The state variables <math>r,v,m</math> describe the altitude, speed and mass. | + | The state variables <math>r,v,m</math> describe the altitude(radius), speed and mass respectively. |
The drag is given by | The drag is given by | ||
| Line 17: | Line 25: | ||
<math> | <math> | ||
\begin{array}{llcll} | \begin{array}{llcll} | ||
| − | \displaystyle \ | + | \displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex] |
\mbox{s.t.} & \dot{r} & = & v, \\ | \mbox{s.t.} & \dot{r} & = & v, \\ | ||
& \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex] | & \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex] | ||
& \dot{m} & = & -b T_{max} u, \\ | & \dot{m} & = & -b T_{max} u, \\ | ||
| − | & u( | + | & u(t) &\in& [0,1] \\ |
& r(0) &=& r_0, \\ | & r(0) &=& r_0, \\ | ||
& v(0) &=& v_0, \\ | & v(0) &=& v_0, \\ | ||
& m(0) &=& m_0, \\ | & m(0) &=& m_0, \\ | ||
& r(T) &=& r_T, \\ | & r(T) &=& r_T, \\ | ||
| − | & D(r | + | & D(r,v)&\le& C \\ |
| − | & T free | + | & T \, free |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Line 61: | Line 69: | ||
Image:Goddartmass.png| Mass m over time. | Image:Goddartmass.png| Mass m over time. | ||
</gallery> | </gallery> | ||
| + | |||
| + | == Source Code == | ||
| + | Model descriptions are available in: | ||
| + | |||
| + | * [[:Category: Bocop | Bocop code]] at [[Goddart's rocket problem (Bocop)]] | ||
| + | * [[:Category: AMPL/TACO | AMPL/TACO code]] at [[Goddart's rocket problem (TACO)]] | ||
| + | |||
| + | == References == | ||
| + | The Problem can be found in the [http://bocop.org/ BOCOP User Guide]. | ||
| + | |||
| + | [[Category:MIOCP]] | ||
| + | [[Category:Aeronautics]] | ||
| + | [[Category:Minimum energy]] | ||
| + | [[Category:ODE model]] | ||
| + | [[Category:Path-constrained arcs]] | ||
| + | [[Category:Sensitivity-seeking arcs]] | ||
Latest revision as of 17:08, 22 February 2016
| Goddart's rocket problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Continuous control functions: | 1 |
| Path constraints: | 1 |
| Interior point equalities: | 4 |
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.
Contents
Variables
The state variables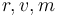 
describe the altitude(radius), speed and mass respectively.
The drag is given by
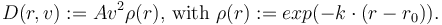
Mathematical formulation
![\begin{array}{llcll}
\displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex]
\mbox{s.t.} & \dot{r} & = & v, \\
& \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex]
& \dot{m} & = & -b T_{max} u, \\
& u(t) &\in& [0,1] \\
& r(0) &=& r_0, \\
& v(0) &=& v_0, \\
& m(0) &=& m_0, \\
& r(T) &=& r_T, \\
& D(r,v)&\le& C \\
& T \, free
\end{array}](https://mintoc.de/images/math/1/5/1/1510d912f548b873254257dbd8da014e.png)
Parameters
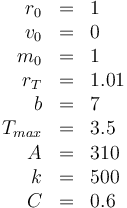
Reference Solution
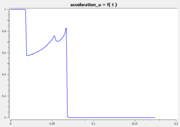
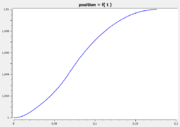
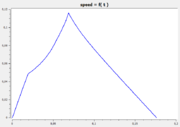
The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389.
- Reference solution plots
Control u over time.
Position r over time.
Speed v over time.
Mass m over time.
Source Code
Model descriptions are available in:
References
The Problem can be found in the BOCOP User Guide.
