Difference between revisions of "Oil Shale Pyrolysis"

From mintOC
Jump to: navigation, search
 
(13 intermediate revisions by 3 users not shown)
Line 1: Line 1:
 
{{Dimensions
 
{{Dimensions
−
|nd        = 1
+
|nd        = 4
−
|nx        = 2
+
|nx        = 4
 
|nu        = 1
 
|nu        = 1
 
|nw        = 0
 
|nw        = 0
−
|nre      = 2
+
|nc        = 4
 +
|nre      = 0
 
}}
 
}}
  
−
The following problem is an example from the global optimal control literature and was introduced in <bib id="Wen1977" />.  
+
The following problem is an example from the global optimal control literature and was introduced in <bib id="Wen1977" />. The process starts with kerogen and is decomposed into pyrolytic bitumen, oil and gas, and residual carbon. The objective is to maximize the fraction of pyrolytic bitumen. There are 5 reactions including:
  
 +
<math>A_1 \xrightarrow{k_1} A_2</math>
  
−
== Mathematical formulation ==
+
<math>A_2 \xrightarrow{k_2} A_3</math>
  
−
<math>
+
<math>A_1 + A_2 \xrightarrow{k_3} A_2 + A_2</math>
−
\begin{array}{ll}
+
−
\displaystyle \min_{u} &  \displaystyle -x_1(t_N)^2  \\[1.5ex]
+
−
\mbox{s.t.} &  \displaystyle \dot{x}_0(t) = -k_0x_0(t)-(k_2+k_3+k_4)x_0(t)x_1(t)\\
+
−
&  \displaystyle \dot{x}_1(t) = k_0x_0(t)-k_1x_1(t) + k_2x_0(t)x_1(t)\\
+
−
&  \displaystyle k_i = a_i e^{-u(t)\frac{b_i}{R}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex]
+
−
&  \displaystyle t \in \left[t_0,t_N\right] \\
+
−
&  \displaystyle u(t) \in \left[698.15/748.15,1\right]\\
+
−
&  \displaystyle x(t_0) = (1,0)^T\\
+
−
\end{array}
+
−
</math>
+
  
−
where this is the normalized form with
+
<math>A_1 + A_2 \xrightarrow{k_4} A_3 + A_2</math>
  
−
<math> u(t)= \frac{1}{u_{temp}} </math>, with
+
<math>A_1 + A_2 \xrightarrow{k_5} A_4 + A_2</math>
  
−
<math> u_{temp} \in \left[698.15,748.15\right] </math>
+
Each reaction is governed by a rate described by:
  
−
== Parameters ==
+
<math>k_i = k_{i0} \exp{\left(-E_i/RT\right)}, (i=1,2,3,4,5)</math>
  
 +
== Mathematical formulation ==
  
 +
<math>
 +
\begin{array}{lll}
 +
\displaystyle \max_{T} &  \displaystyle &x_2(t_N)  \\[1.5ex]
 +
\mbox{s.t.} &  \displaystyle \dot{x}_1 &= -k_1x_1-(k_3+k_4+k_5)x_1x_2\\
 +
&  \displaystyle \dot{x}_2 &= k_1x_1-k_2x_2 + k_3x_1x_2\\
 +
&  \displaystyle \dot{x}_3 &= k_2x_2 + k_4x_1x_2\\
 +
&  \displaystyle \dot{x}_4 &= k_5x_1x_2\\
 +
&  \displaystyle k_i &= a_i e^{-\frac{b_i}{RT}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex]
 +
&  \displaystyle t &\in \left[t_0,t_N\right] \\
 +
&  \displaystyle T(t) &\in \left[698.15K,748.15K\right]\\
 +
&  \displaystyle x(t_0) &= (1,0,0,0)^T\\
 +
\end{array}
 +
</math>
 +
 +
== Parameters ==
  
 
{| class="wikitable"
 
{| class="wikitable"
Line 40: Line 48:
 
|Initial value (<math>t_0</math>)
 
|Initial value (<math>t_0</math>)
 
|-
 
|-
−
|<math>x_0(t)</math>
+
|<math>x_1(t_0)</math>
 
|<math>1</math>
 
|<math>1</math>
 
|-
 
|-
−
|<math>x_1(t)</math>
+
|<math>x_2(t_0)</math>
 +
|<math>0 </math>
 +
|-
 +
|<math>x_3(t_0)</math>
 +
|<math>0 </math>
 +
|-
 +
|<math>x_4(t_0)</math>
 
|<math>0 </math>
 
|<math>0 </math>
 
|}
 
|}
Line 54: Line 68:
 
|-
 
|-
 
|<math>a_1</math>
 
|<math>a_1</math>
−
|<math>8.86</math>
+
|<math>20.3</math>
 
|-
 
|-
 
|<math>a_2</math>
 
|<math>a_2</math>
−
|<math>24.25</math>
+
|<math>37.4</math>
 
|-
 
|-
 
|<math>a_3</math>
 
|<math>a_3</math>
−
|<math>23.67</math>
+
|<math>33.8</math>
 
|-
 
|-
 
|<math>a_4</math>
 
|<math>a_4</math>
−
|<math>18.75</math>
+
|<math>28.2</math>
 
|-
 
|-
 
|<math>a_5</math>
 
|<math>a_5</math>
−
|<math>20.7</math>
+
|<math>31.0</math>
 
|-
 
|-
 
|<math>b_1</math>
 
|<math>b_1</math>
−
|<math>20.3</math>
+
|<math>\exp{(8.86)}</math>
 
|-
 
|-
 
|<math>b_2</math>
 
|<math>b_2</math>
−
|<math>37.4</math>
+
|<math>\exp{(24.25)}</math>
 
|-
 
|-
 
|<math>b_3</math>
 
|<math>b_3</math>
−
|<math>33.8</math>
+
|<math>\exp{(23.67)}</math>
 
|-
 
|-
 
|<math>b_4</math>
 
|<math>b_4</math>
−
|<math>28.2</math>
+
|<math>\exp{(18.75)}</math>
 
|-
 
|-
 
|<math>b_5</math>
 
|<math>b_5</math>
−
|<math>31.0</math>
+
|<math>\exp{(20.7)}</math>
 
|}
 
|}
  
Line 90: Line 104:
 
|Interval
 
|Interval
 
|-
 
|-
−
|<math>u(t)</math>
+
|<math>T(t)</math>
−
|[698.15/748.15,1]
+
|[698.15,748.15]
 
|}
 
|}
  
−
'''Measurement grid'''
+
== Solutions ==
−
 
+
−
== Reference solution ==
+
−
 
+
−
Coming soon.
+
−
 
+
−
== Source Code ==
+
−
 
+
−
Model descriptions are available in
+
−
 
+
−
* [[:Category:GloOptCon | GloOptCon code]] at [[Oil Shale Pyrolysis (GloOptCon)]]
+
  
 +
* [[:Category:Gekko | GEKKO Python code]] at [[Oil shale pyrolysis (GEKKO)]]
  
 
== References ==
 
== References ==
 
<biblist />
 
<biblist />
  
−
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
+
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, or presence of implementation details (e.g., AMPL for AMPL model) here -->
 
[[Category:MIOCP]]
 
[[Category:MIOCP]]
−
[[Category:GloOptCon]]
+
[[Category:ODE model]]

Latest revision as of 03:02, 15 March 2019

Oil Shale Pyrolysis
State dimension: 4
Differential states: 4
Continuous control functions: 1
Discrete control functions: 0
Path constraints: 4
Interior point equalities: 0


The following problem is an example from the global optimal control literature and was introduced in [Wen1977]The entry doesn't exist yet.. The process starts with kerogen and is decomposed into pyrolytic bitumen, oil and gas, and residual carbon. The objective is to maximize the fraction of pyrolytic bitumen. There are 5 reactions including:

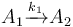
A_1 \xrightarrow{k_1} A_2

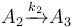
A_2 \xrightarrow{k_2} A_3

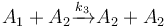
A_1 + A_2 \xrightarrow{k_3} A_2 + A_2

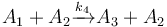
A_1 + A_2 \xrightarrow{k_4} A_3 + A_2

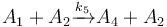
A_1 + A_2 \xrightarrow{k_5} A_4 + A_2

Each reaction is governed by a rate described by:

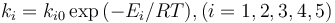
k_i = k_{i0} \exp{\left(-E_i/RT\right)}, (i=1,2,3,4,5)

Mathematical formulation

\begin{array}{lll} \displaystyle \max_{T} & \displaystyle &x_2(t_N) \\[1.5ex] \mbox{s.t.} & \displaystyle \dot{x}_1 &= -k_1x_1-(k_3+k_4+k_5)x_1x_2\\ & \displaystyle \dot{x}_2 &= k_1x_1-k_2x_2 + k_3x_1x_2\\ & \displaystyle \dot{x}_3 &= k_2x_2 + k_4x_1x_2\\ & \displaystyle \dot{x}_4 &= k_5x_1x_2\\ & \displaystyle k_i &= a_i e^{-\frac{b_i}{RT}},\quad \forall i\in \{1,\dots,5\} \\ [1.5ex] & \displaystyle t &\in \left[t_0,t_N\right] \\ & \displaystyle T(t) &\in \left[698.15K,748.15K\right]\\ & \displaystyle x(t_0) &= (1,0,0,0)^T\\ \end{array}

Parameters

State variables
Symbol Initial value (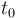t_0)
x_1(t_0) 1
x_2(t_0) 0
x_3(t_0) 0
x_4(t_0) 0
Parameters
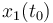
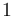
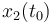
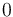
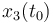
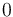
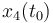
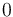
Symbol Value
a_1 20.3
a_2 37.4
a_3 33.8
a_4 28.2
a_5 31.0
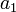
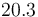
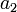
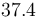
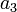
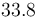
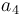
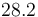
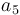
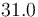
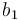
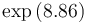
b_1 \exp{(8.86)}
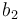
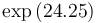
b_2 \exp{(24.25)}
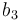
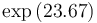
b_3 \exp{(23.67)}
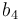
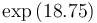
b_4 \exp{(18.75)}
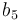
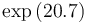
b_5 \exp{(20.7)}
Control variable
Symbol Interval
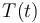
T(t) [698.15,748.15]

Solutions

References

[Wen1977]The entry doesn't exist yet.
Retrieved from "https://mintoc.de/index.php?title=Oil_Shale_Pyrolysis&oldid=2281"