Difference between revisions of "Hanging chain problem"
From mintOC
FelixMueller (Talk | contribs) (→Parameters) |
(→Source Code) |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{Dimensions | {{Dimensions | ||
|nd = 1 | |nd = 1 | ||
| − | |nx = | + | |nx = 3 |
| − | | | + | |nu = 1 |
| − | |nre = | + | |nc = 4 |
| + | |nre = 5 | ||
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... | ||
| Line 33: | Line 34: | ||
In this model the parameters used are | In this model the parameters used are | ||
| + | |||
<math> | <math> | ||
\begin{array}{rcl} | \begin{array}{rcl} | ||
[t_0, t_f] &=& [0, 1],\\ | [t_0, t_f] &=& [0, 1],\\ | ||
| − | (a,b) &=& ( | + | (a,b) &=& (1,3),\\ |
Lp &=& 4. | Lp &=& 4. | ||
\end{array} | \end{array} | ||
| Line 46: | Line 48: | ||
* [[:Category:AMPL/TACO | AMPL/TACO code]] at [[Hanging chain problem (TACO)]] | * [[:Category:AMPL/TACO | AMPL/TACO code]] at [[Hanging chain problem (TACO)]] | ||
| − | + | * [[:Category:Gekko | GEKKO Python code]] at [[Hanging chain problem (GEKKO)]] | |
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> | <!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> | ||
[[Category:MIOCP]] | [[Category:MIOCP]] | ||
[[Category:ODE model]] | [[Category:ODE model]] | ||
| − | [[Category: | + | [[Category:Minimum energy]] |
Latest revision as of 20:19, 13 March 2019
| Hanging chain problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Continuous control functions: | 1 |
| Path constraints: | 4 |
| Interior point equalities: | 5 |
The Hanging chain problem is concerned with finding a chain (of uniform density) of length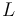 
suspendend between two points 
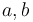with minimal potential energy. (Problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, u} & x_2(t_f) \\[1.5ex]
\mbox{s.t.} & \dot{x}_1 & = & u, \\
& \dot{x}_2 & = & x_1 (1+u^2)^{1/2}, \\
& \dot{x}_3 & = & (1+u^2)^{1/2}, \\
& x(t_0) &=& (a,0,0)^T, \\
& x_1(t_f) &=& b, \\
& x_3(t_f) &=& Lp, \\
& x(t) &\in& [0,10], \\
& u(t) &\in& [-10,20].
\end{array}](https://mintoc.de/images/math/b/c/7/bc780667f14aed98c5f25693189fe3bb.png)
Parameters
In this model the parameters used are
![\begin{array}{rcl}
[t_0, t_f] &=& [0, 1],\\
(a,b) &=& (1,3),\\
Lp &=& 4.
\end{array}](https://mintoc.de/images/math/e/e/0/ee0e9c5601a4e38d2c026c83b4756eb8.png)
Source Code
Model descriptions are available in
