Difference between revisions of "Isomerization of Alpha-Pinene problem"

From mintOC
Jump to: navigation, search
 
(4 intermediate revisions by the same user not shown)
Line 2: Line 2:
 
|nz        = 5
 
|nz        = 5
 
|np        = 5
 
|np        = 5
 +
|nc        = 5
 
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout...
 
}}<!-- Do not insert line break here or Dimensions Box moves up in the layout...
  
Line 21: Line 22:
 
  & \dot{y}_3 & = & \theta_2 y_1 - (\theta_3 + \theta_4) y_3 + \theta_5 y_5,  \\
 
  & \dot{y}_3 & = & \theta_2 y_1 - (\theta_3 + \theta_4) y_3 + \theta_5 y_5,  \\
 
  & \dot{y}_4 & = & \theta_3 y_3,  \\
 
  & \dot{y}_4 & = & \theta_3 y_3,  \\
−
  & \dot{y}_5 & = & \theta_4 y_3 - \theta_5 y_5. \\
+
  & \dot{y}_5 & = & \theta_4 y_3 - \theta_5 y_5, \\
 +
  & \theta_i & \geq & 0 \quad i = 1,...,5.
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
Line 39: Line 41:
 
[[Category:MIOCP]]
 
[[Category:MIOCP]]
 
[[Category:ODE model]]
 
[[Category:ODE model]]
 +
[[Category:DAE model]]
 +
[[Category:Chemical engineering]]

Latest revision as of 20:22, 29 September 2016

Isomerization of Alpha-Pinene problem
Algebraic states: 5
Continuous control values: 5
Path constraints: 5

The Isomerization of Alpha-Pinene problem tries to determine "reaction coefficients in the thermal isometrization of 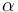\alpha -Pinene." (Cite and problem taken from the COPS library)


Mathematical formulation

The problem is given by

\begin{array}{llcl} \displaystyle \min_{\theta} &\sum\limits_{j=1}^{8} &&||y(\tau_j; \theta) - z_j||^2 \\[1.5ex] \mbox{s.t.} & \dot{y}_1 & = & -(\theta_1 + \theta_2) y_1, \\ & \dot{y}_2 & = & \theta_1 y_1, \\ & \dot{y}_3 & = & \theta_2 y_1 - (\theta_3 + \theta_4) y_3 + \theta_5 y_5, \\ & \dot{y}_4 & = & \theta_3 y_3, \\ & \dot{y}_5 & = & \theta_4 y_3 - \theta_5 y_5, \\ & \theta_i & \geq & 0 \quad i = 1,...,5. \end{array}

Parameters

The values 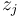z_j are measurements for the concentration for 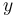y at time points \tau_1, ..., \tau_8 and initial conditions are known.

Source Code

Model descriptions are available in

Retrieved from "https://mintoc.de/index.php?title=Isomerization_of_Alpha-Pinene_problem&oldid=2147"