|
|
| (2 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| − | The '''GEKKO''' Python package<ref>{{cite journal | last=Beal | first=L. | title=GEKKO Optimization Suite | journal=Processes | year=2018 | doi=10.3390/pr6080106 | volume=6 | number=8 | pages=106}}</ref> solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers ([[IPOPT]], [[APOPT]], BPOPT, [[SNOPT]], [[MINOS_(optimization_software)|MINOS]]). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear [[Model_predictive_control|model predictive control]]. In addition, the package solves [[Linear programming]] (LP), [[Quadratic programming]] (QP), [[Quadratically constrained quadratic program]] (QCQP), [[Nonlinear programming]] (NLP), [[Mixed integer programming]] (MIP), and [[Mixed integer linear programming]] (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation. | + | The '''GEKKO''' Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (IPOPT, APOPT, BPOPT, SNOPT, MINOS). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation. |
| | | | |
| | <source lang="python"> | | <source lang="python"> |
| Line 5: |
Line 5: |
| | </source> | | </source> |
| | | | |
| − | GEKKO works on all platforms (Windows, MacOS, Linux, ARM processors) and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There is a Windows and Linux option to solve without an Internet connection. GEKKO is an extension of the [[APMonitor|APMonitor Optimization Suite]] but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71<ref>W. Hock and K. Schittkowski, Test Examples for Nonlinear Programming Codes, Lecture Notes in Economics and Mathematical Systems, Vol. 187, Springer 1981.</ref> used to test the performance of [[nonlinear programming]] solvers. This particular optimization problem has an objective function <math>\min_{x\in\mathbb R}\; x_1 x_4 (x_1+x_2+x_3)+x_3</math> and subject to the inequality constraint <math>x_1 x_2 x_3 x_4 \ge 25</math> and equality constraint <math>{x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2=40</math>. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are <math>x_1 = 1, x_2=5, x_3=5, x_4=1</math>. This optimization problem is solved with GEKKO as shown below. | + | GEKKO works on all platforms (Windows, MacOS, Linux, ARM processors) and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There is a Windows and Linux option to solve without an Internet connection. GEKKO is an extension of the APMonitor Optimization Suite but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71 used to test the performance of nonlinear programming solvers. This particular optimization problem has an objective function <math>\min_{x\in\mathbb R}\; x_1 x_4 (x_1+x_2+x_3)+x_3</math> and subject to the inequality constraint <math>x_1 x_2 x_3 x_4 \ge 25</math> and equality constraint <math>{x_1}^2 + {x_2}^2 + {x_3}^2 + {x_4}^2=40</math>. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are <math>x_1 = 1, x_2=5, x_3=5, x_4=1</math>. This optimization problem is solved with GEKKO as shown below. |
| | | | |
| | <source lang="python"> | | <source lang="python"> |
| Line 26: |
Line 26: |
| | print('Objective: ' + str(m.options.objfcnval)) | | print('Objective: ' + str(m.options.objfcnval)) |
| | </source> | | </source> |
| − |
| |
| − | ==Applications of GEKKO==
| |
| − |
| |
| − | Applications include [[Cogeneration|cogeneration (power and heat)]]<ref>{{cite journal | last=Mojica | first=J. | title=Optimal combined long-term facility design and short-term operational strategy for CHP capacity investments | journal=Energy | year=2017 | doi=10.1016/j.energy.2016.12.009 | volume=118 | pages=97–115}}</ref>, [[Oil well|drilling automation]]<ref>{{cite journal | last=Eaton | first=A. | title=Real time model identification using multi-fidelity models in managed pressure drilling | journal=Computers & Chemical Engineering | year=2017 | doi=10.1016/j.compchemeng.2016.11.008 | volume=97 | pages=76–84}}</ref>, severe slugging control<ref>{{cite journal | last=Eaton | first=A. | title=Post-installed fiber optic pressure sensors on subsea production risers for severe slugging control | journal=OMAE 2015 Proceedings, St. John's, Canada | year=2015 | url=http://apm.byu.edu/prism/uploads/Projects/Eaton_OMAE15.pdf}}</ref>, solar thermal energy production<ref>{{cite journal | last=Powell | first=K. | title=Dynamic Optimization of a Hybrid Solar Thermal and Fossil Fuel System | journal=Solar Energy | year=2014 | doi=10.1016/j.solener.2014.07.004 | volume=108 | pages=210–218}}</ref>, [[solid oxide fuel cell]]s<ref>{{cite journal | last=Spivey | first=B. | title=Dynamic Modeling of Reliability Constraints in Solid Oxide Fuel Cells and Implications for Advanced Control | journal=AIChE Annual Meeting Proceedings, Salt Lake City, Utah | year=2010 | url=http://apmonitor.com/wiki/uploads/Apps/sofc.pdf}}</ref><ref>{{cite journal | last=Spivey | first=B. | title=Dynamic modeling, simulation, and MIMO predictive control of a tubular solid oxide fuel cell | journal=Journal of Process Control | year=2012 | doi=10.1016/j.jprocont.2012.01.015 | volume=22 | issue=8 | pages=1502–1520}}</ref>, flow assurance <ref>{{cite journal | last=Hedengren | first=J. | title=New flow assurance system with high speed subsea fiber optic monitoring of pressure and temperature | journal=ASME 37th International Conference on Ocean, Offshore and Arctic Engineering, OMAE2018/78079, Madrid, Spain | pages=V005T04A034 | year=2018| doi=10.1115/OMAE2018-78079 | isbn=978-0-7918-5124-1 }}</ref>, [[Enhanced oil recovery]] <ref>{{cite journal | last=Udy | first=J. | title=Reduced order modeling for reservoir injection optimization and forecasting | journal=FOCAPO / CPC 2017, Tuscon, AZ | year=2017 | url=https://apm.byu.edu/prism/uploads/Members/udy2017_eor.pdf}}</ref>, [[Essential oil]] extraction<ref>{{cite journal | last=Valderrama | first=F. | title=An optimal control approach to steam distillation of essential oils from aromatic plants | journal=Computers & Chemical Engineering | volume=117 | pages=25–31 | year=2018 | doi=10.1016/j.compchemeng.2018.05.009 }}</ref>, and [[Unmanned aerial vehicle|Unmanned Aerial Vehicles (UAVs)]]<ref>{{cite journal | last=Sun | first=L. | title=Optimal Trajectory Generation using Model Predictive Control for Aerially Towed Cable Systems | journal=Journal of Guidance, Control, and Dynamics | year=2013 | url=http://apm.byu.edu/prism/uploads/Members/sun_2013.pdf}}</ref>. There are many other references to [http://apmonitor.com/wiki/index.php/Main/APMonitorReferences APMonitor and GEKKO] as a sample of the types of applications that can be solved. GEKKO is developed from the National Science Foundation (NSF) research grant #1547110 <ref>{{cite journal | last=Beal | first=L. | title=Integrated scheduling and control in discrete-time with dynamic parameters and constraints | journal=Computers & Chemical Engineering | volume=115 | pages=361–376 | year=2018 | doi=10.1016/j.compchemeng.2018.04.010}}</ref><ref>{{cite journal | last=Beal | first=L. | title=Combined model predictive control and scheduling with dominant time constant compensation | journal=Computers & Chemical Engineering | volume=104 | pages=271–282 | year=2017 | url=https://scholarsarchive.byu.edu/facpub/1905/ | doi=10.1016/j.compchemeng.2017.04.024}}</ref><ref>{{cite journal | last=Beal | first=L. | title=Economic benefit from progressive integration of scheduling and control for continuous chemical processes | journal=Processes | year=2017 | doi=10.3390/pr5040084 | volume=5| issue=4 | pages=84 }}</ref><ref>{{cite journal | last=Petersen | first=D. | title=Combined noncyclic scheduling and advanced control for continuous chemical processes | journal=Processes | year=2017 | doi=10.3390/pr5040083 | volume=5| issue=4 | pages=83 }}</ref> and is detailed in a Special Issue collection on combined scheduling and control<ref>{{cite journal | last=Hedengren | first=J. | title=Special issue: combined scheduling and control | journal=Processes | volume=6 | issue=3 | pages=24 | year=2018 | url=http://www.mdpi.com/journal/processes/special_issues/Combined_Scheduling | doi=10.3390/pr6030024}}</ref>. Other notable mentions of GEKKO are the listing in the Decision Tree for Optimization Software<ref>{{cite web |url=http://plato.asu.edu/sub/tools.html |title=Decision Tree for Optimization Software |last=Mittleman |first=Hans |date=1 May 2018 |website=Plato |publisher=Arizona State University |access-date=1 May 2018
| |
| − | |quote=Object-oriented python library for mixed-integer and differential-algebraic equations}}</ref>, added support for [[APOPT]] and BPOPT solvers<ref>{{cite web
| |
| − | |url=https://apopt.com |title=Solver Solutions |publisher=Advanced Process Solutions, LLC |access-date=1 May 2018 |quote=GEKKO Python with APOPT or BPOPT Solvers}}</ref>, projects reports of the online Dynamic Optimization course from international participants<ref>{{cite web |url=http://apmonitor.com/do/index.php/Main/ProjectLab |title=Dynamic Optimization Projects |last=Everton |first=Colling |website=Petrobras |publisher=Petrobras, Statoil, Facebook |access-date=1 May 2018 |quote=Example Presentation: Everton Colling of Petrobras shares his experience with GEKKO for modeling and nonlinear control of distillation}}</ref>. GEKKO is a topic in online forums where users are solving optimization and optimal control problems<ref>{{cite web |url=https://groups.google.com/forum/#!searchin/apmonitor/gekko |title=APMonitor Google Group: GEKKO |website=Google |access-date=1 May 2018}}</ref><ref>{{cite web |url=https://scicomp.stackexchange.com/questions/83/is-there-a-high-quality-nonlinear-programming-solver-for-python |title=Computational Science: Is there a high quality nonlinear programming solver for Python? |website=SciComp |access-date=1 May 2018}}</ref>. GEKKO is used for advanced control in the Temperature Control Lab (TCLab)<ref>{{cite web |url=https://media.readthedocs.org/pdf/tclab/stable/tclab.pdf |title=TCLab Documentation |last=Kantor |first=Jeff |date=2 May 2018 |website=ReadTheDocs |publisher=University of Notre Dame |access-date=2 May 2018
| |
| − | |quote=pip install tclab}}</ref> for process control education at 20 universities<ref>{{cite web |url=https://jckantor.github.io/CBE30338/ |title=Chemical Process Control |last=Kantor |first=Jeff |date=2 May 2018 |website=GitHub |publisher=University of Notre Dame |access-date=2 May 2018
| |
| − | |quote=Using the Temperature Control Lab (TCLab)}}</ref><ref>{{cite web |url=http://apmonitor.com/do/index.php/Main/AdvancedTemperatureControl |title=Advanced Temperature Control Lab |last=Hedengren |first=John |date=2 May 2018 |website=Dynamic Optimization Course |publisher=Brigham Young University |access-date=2 May 2018 |quote=Hands-on applications of advanced temperature control}}</ref><ref>{{cite web |url=https://github.com/alchemyst/Dynamics-and-Control |title=Jupyter notebooks for Dynamics and Control |last=Sandrock |first=Carl |date=2 May 2018 |website=GitHub |publisher=University of Pretoria, South Africa |access-date=2 May 2018 |quote=CPN321 (Process Dynamics), and CPB421 (Process Control) at the Chemical Engineering department of the University of Pretoria}}</ref><ref>{{cite web |url=http://cache.org/files/winter-2018-dynamic-simulation.pdf |title=CACHE News (Winter 2018): Incorporating Dynamic Simulation into Chemical Engineering Curricula |date=2 May 2018 |website=CACHE: Computer Aids for Chemical Engineering |publisher=University of Texas at Austin |access-date=2 May 2018 |quote=Short Course at the ASEE 2017 Summer School hosted at SCSU by Hedengren (BYU), Grover (Georgia Tech), and Badgwell (ExxonMobil)}}</ref>.
| |
| − |
| |
| − | ==References==
| |
| − | {{reflist}}
| |
| | | | |
| | == External links == | | == External links == |
| | + | * [https://en.wikipedia.org/wiki/Gekko_(optimization_software) GEKKO on Wikipedia] |
| | * [https://gekko.readthedocs.io/en/latest/ GEKKO Documentation] | | * [https://gekko.readthedocs.io/en/latest/ GEKKO Documentation] |
| | * [https://github.com/BYU-PRISM/GEKKO GEKKO Source Code] | | * [https://github.com/BYU-PRISM/GEKKO GEKKO Source Code] |
Latest revision as of 21:08, 13 March 2019
The GEKKO Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (IPOPT, APOPT, BPOPT, SNOPT, MINOS). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation.
GEKKO works on all platforms (Windows, MacOS, Linux, ARM processors) and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There is a Windows and Linux option to solve without an Internet connection. GEKKO is an extension of the APMonitor Optimization Suite but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71 used to test the performance of nonlinear programming solvers. This particular optimization problem has an objective function 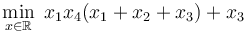 and subject to the inequality constraint
and subject to the inequality constraint 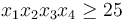 and equality constraint
and equality constraint 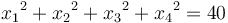 . The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are
. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are 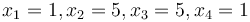 . This optimization problem is solved with GEKKO as shown below.
. This optimization problem is solved with GEKKO as shown below.
from gekko import GEKKO
m = GEKKO() # Initialize gekko
# Initialize variables
x1 = m.Var(value=1,lb=1,ub=5)
x2 = m.Var(value=5,lb=1,ub=5)
x3 = m.Var(value=5,lb=1,ub=5)
x4 = m.Var(value=1,lb=1,ub=5)
# Equations
m.Equation(x1*x2*x3*x4>=25)
m.Equation(x1**2+x2**2+x3**2+x4**2==40)
m.Obj(x1*x4*(x1+x2+x3)+x3) # Objective
m.solve(disp=False) # Solve
print('x1: ' + str(x1.value))
print('x2: ' + str(x2.value))
print('x3: ' + str(x3.value))
print('x4: ' + str(x4.value))
print('Objective: ' + str(m.options.objfcnval))External links
Pages in category "Gekko"
The following 6 pages are in this category, out of 6 total.
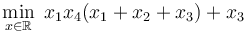 and subject to the inequality constraint
and subject to the inequality constraint 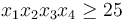 and equality constraint
and equality constraint 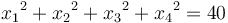 . The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are
. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are 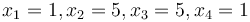 . This optimization problem is solved with GEKKO as shown below.
. This optimization problem is solved with GEKKO as shown below.