Difference between revisions of "Category:Periodic"
From mintOC
m (Periodicity constraint is a characteristic of the optimization task, not of the optimal solution. Added operation P().) |
m |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | This is a category with all control problems that seek | + | This is a category with all control problems that seek periodic solutions, i.e., a condition of the kind |
| − | <math> | + | <center><math> |
| − | x | + | \Gamma[x] = P(x(t_f)) - x(t_0) = 0, |
| − | </math> | + | </math></center> |
| − | has to hold. <math>P(\cdot)</math> is an operation that allows, e.g., for a perturbation of states | + | has to hold. <math>P(\cdot)</math> is an operation that allows, e.g., for a perturbation of states, such as needed for the formulation of [[:Category:Simulated moving bed | Simulated moving bed]] processes, or for offsets of angles by a multiple of <math>2 \pi</math> such as in [[Car testdrive (elliptic track) | periodic car driving]]. |
| − | [[Category: | + | [[Category:Objective characterization]] |
Latest revision as of 12:52, 20 November 2010
This is a category with all control problems that seek periodic solutions, i.e., a condition of the kind
![\Gamma[x] = P(x(t_f)) - x(t_0) = 0,](https://mintoc.de/images/math/d/8/1/d8164876021ddaee384c20b676100dc7.png)
has to hold.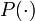 
is an operation that allows, e.g., for a perturbation of states, such as needed for the formulation of Simulated moving bed processes, or for offsets of angles by a multiple of 
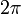such as in periodic car driving.
Pages in category "Periodic"
The following 2 pages are in this category, out of 2 total.
