Difference between revisions of "Supermarket refrigeration system"

From mintOC
Jump to: navigation, search
(Undo revision 354 by AlexanderBuchner (Talk))
 
(19 intermediate revisions by 5 users not shown)
Line 2: Line 2:
 
|nd        = 1
 
|nd        = 1
 
|nx        = 9
 
|nx        = 9
−
|nw        = 4
+
|nw        = 3
−
|nri       = 5
+
|nc        = 7
 +
|nre       = 9
 
}}
 
}}
  
Line 10: Line 11:
 
The air temperatures surrounding the goods in each display case are modeled by one differential state each. These states have to be bounded, so that the goods are properly refrigerated.
 
The air temperatures surrounding the goods in each display case are modeled by one differential state each. These states have to be bounded, so that the goods are properly refrigerated.
  
−
The model was published by Larsen et. al. in 2007 <bibref>Larsen2007</bibref>. The main goal is to control the refirgeration system energy-optimal. The problem was set up as a benchmark problem for MIOCPs.  
+
The model was published by Larsen et. al. in 2007 <bib id="Larsen2007" />. The main goal is to control the refirgeration system energy-optimal. The problem was set up as a benchmark problem for MIOCPs.  
  
 
The mathematical equations form an [[:Category:ODE model|ODE model]]. The initial values of the differential states are not fixed but periodicity of the whole process is required.
 
The mathematical equations form an [[:Category:ODE model|ODE model]]. The initial values of the differential states are not fixed but periodicity of the whole process is required.
  
−
The optimal integer control functions shows [[:Category:Chattering|chattering]] behavior, making the supermarket refrigeration system problem a candidate for benchmarking of algorithms.
+
The optimal integer control function shows [[:Category:Chattering|chattering]] behavior, making the supermarket refrigeration system problem a candidate for benchmarking of algorithms.
  
 
== Mathematical formulation ==
 
== Mathematical formulation ==
Line 20: Line 21:
 
For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by
 
For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by
  
−
 
+
<p>
 
<math>
 
<math>
−
\min_{x,u} \frac {1}{t_f - t_0}\int_{t_0}^{t_f} \left( (u_2 + u_3)\cdot 0.5 \cdot \eta_{vol} \cdot V_{sl} \cdot f \right) dt  
+
\min_{x,u} \frac {1}{t_f - t_0}\int_{t_0}^{t_f} \left( u_2 \cdot 0.5 \cdot \eta_{vol} \cdot V_{sl} \cdot f \right) dt  
 
</math>
 
</math>
 +
</p>
  
 +
<p>
 
<math>
 
<math>
 
\begin{array}{llcl}
 
\begin{array}{llcl}
 
  \displaystyle  
 
  \displaystyle  
 
  \mbox{s.t.} &  
 
  \mbox{s.t.} &  
−
\dot{x_0}(t) &=&  \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[  
+
\dot{x_0} &=&  \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[  
 
                     \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot
 
                     \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot
 
                     \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\  
 
                     \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\  
−
&          &&  + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const}  - \eta_{vol} \cdot V_{sl} \cdot 0.5 \, \left(u_2+u_3\right) \rho_{suc}(x_0)  
+
&          &&  + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const}  - \eta_{vol} \cdot V_{sl} \cdot 0.5 \, u_2 \rho_{suc}(x_0)  
 
                 \bigg] \\
 
                 \bigg] \\
−
  &\dot{x_1}(t) &=&  - \dfrac{
+
  &\dot{x_1} &=&  - \dfrac{
 
                     UA_{goods-air} \left( x_1 - x_3 \right)
 
                     UA_{goods-air} \left( x_1 - x_3 \right)
 
}{
 
}{
 
                     M_{goods} \cdot C_{p,goods}  
 
                     M_{goods} \cdot C_{p,goods}  
 
} \\  
 
} \\  
−
  &\dot{x_2}(t) &=&  \dfrac{
+
  &\dot{x_2} &=&  \dfrac{
 
                     UA_{air-wall} \left( x_3-x_2 \right)
 
                     UA_{air-wall} \left( x_3-x_2 \right)
 
                     - \dfrac{UA_{wall-ref,max}}{M_{ref,max}}
 
                     - \dfrac{UA_{wall-ref,max}}{M_{ref,max}}
Line 46: Line 49:
 
                     M_{wall} \cdot C_{p,wall}
 
                     M_{wall} \cdot C_{p,wall}
 
} \\ [2.5ex]
 
} \\ [2.5ex]
−
&\dot{x_3}(t) &=&  \dfrac{
+
&\dot{x_3} &=&  \dfrac{
 
                     UA_{goods-air} \left( x_1-x_3 \right) + \dot{Q}_{airload}
 
                     UA_{goods-air} \left( x_1-x_3 \right) + \dot{Q}_{airload}
 
                     - UA_{air-wall} \, (x_3-x_2)
 
                     - UA_{air-wall} \, (x_3-x_2)
Line 52: Line 55:
 
                     M_{air} \cdot C_{p,air}
 
                     M_{air} \cdot C_{p,air}
 
} \\ [2.5ex]
 
} \\ [2.5ex]
−
&\dot{x_4}(t) &=&  \left(\dfrac{M_{ref,max} - x_4}{\tau_{fill}} \right) u_0
+
&\dot{x_4} &=&  \left(\dfrac{M_{ref,max} - x_4}{\tau_{fill}} \right) u_0
 
                     - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \,
 
                     - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \,
 
                     x_4 \big( x_2 - T_e(x_0) \big) \right) (1-u_0)
 
                     x_4 \big( x_2 - T_e(x_0) \big) \right) (1-u_0)
 
                 \\ \\
 
                 \\ \\
−
&\dot{x_5}(t) &=&  - \dfrac{
+
&\dot{x_5} &=&  - \dfrac{
 
                     UA_{goods-air} \left( x_5 - x_7 \right)
 
                     UA_{goods-air} \left( x_5 - x_7 \right)
 
}{
 
}{
 
                     M_{goods} \cdot C_{p,goods}  
 
                     M_{goods} \cdot C_{p,goods}  
 
} \\  
 
} \\  
−
  &\dot{x_6}(t) &=&  \dfrac{
+
  &\dot{x_6} &=&  \dfrac{
 
                     UA_{air-wall} \left( x_7-x_6 \right)
 
                     UA_{air-wall} \left( x_7-x_6 \right)
 
                     - \dfrac{UA_{wall-ref,max}}{M_{ref,max}}
 
                     - \dfrac{UA_{wall-ref,max}}{M_{ref,max}}
Line 68: Line 71:
 
                     M_{wall} \cdot C_{p,wall}
 
                     M_{wall} \cdot C_{p,wall}
 
} \\ [2.5ex]
 
} \\ [2.5ex]
−
&\dot{x_7}(t) &=&  \dfrac{
+
&\dot{x_7} &=&  \dfrac{
 
                     UA_{goods-air} \left( x_5-x_7 \right) + \dot{Q}_{airload}
 
                     UA_{goods-air} \left( x_5-x_7 \right) + \dot{Q}_{airload}
 
                     - UA_{air-wall} \, (x_7-x_6)
 
                     - UA_{air-wall} \, (x_7-x_6)
Line 74: Line 77:
 
                     M_{air} \cdot C_{p,air}
 
                     M_{air} \cdot C_{p,air}
 
} \\ [2.5ex]
 
} \\ [2.5ex]
−
&\dot{x_8}(t) &=&  \left(\dfrac{M_{ref,max} - x_8}{\tau_{fill}} \right) u_1
+
&\dot{x_8} &=&  \left(\dfrac{M_{ref,max} - x_8}{\tau_{fill}} \right) u_1
 
                     - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \,
 
                     - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \,
 
                     x_8 \big( x_6 - T_e(x_0) \big) \right) (1-u_1)
 
                     x_8 \big( x_6 - T_e(x_0) \big) \right) (1-u_1)
 
                 \\ [4ex]
 
                 \\ [4ex]
  
−
  & x_3(t) &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\
+
  & x_3 &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\
−
  & x_3(t) &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\
+
  & x_3 &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\
−
  & x_7(t) &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\
+
  & x_7 &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\
−
  & x_7(t) &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\
+
  & x_7 &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\
−
  & x_0(t) &\leq& 1.7 \quad \forall t \in [t_0, t_f], \\
+
  & x_0 &\leq& 1.7 \quad \forall t \in [t_0, t_f], \\
 
  & x_i(t_0) &=& free \quad \forall i \in \{0,\dots, 8\}, \\
 
  & x_i(t_0) &=& free \quad \forall i \in \{0,\dots, 8\}, \\
 
  & x_i(t_f) &=& x_i(t_0) \quad \forall i \in \{0,\dots, 8\}, \\
 
  & x_i(t_f) &=& x_i(t_0) \quad \forall i \in \{0,\dots, 8\}, \\
−
  & u_i(t)  &\in&  \{0, 1\} \quad \forall i \in \{0,\dots, 3\}, \\
+
  & u_i(t)  &\in&  \{0, 1\} \quad \forall i \in \{0,\dots, 2\}, \\
 
  & t_f    &\in& [ 650, 750 ].  
 
  & t_f    &\in& [ 650, 750 ].  
  
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
−
 
+
</p>
  
  
Line 103: Line 106:
 
The following polynomial functions are used in the model description originating from interpolations:
 
The following polynomial functions are used in the model description originating from interpolations:
  
 +
<p>
 
<math>
 
<math>
 
\begin{array}{rcl}
 
\begin{array}{rcl}
Line 111: Line 115:
 
\frac{d\rho_{suc}}{dP_{suc}}(x_0)    &=& -0.0329 {x_0}^3 + 0.2161 {x_0}^2 - 0.4742 x_0 + 5.4817,\\
 
\frac{d\rho_{suc}}{dP_{suc}}(x_0)    &=& -0.0329 {x_0}^3 + 0.2161 {x_0}^2 - 0.4742 x_0 + 5.4817,\\
 
f(x_0)                              &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5.
 
f(x_0)                              &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5.
−
 
−
 
−
 
 
\end{array}  
 
\end{array}  
 
</math>
 
</math>
 +
</p>
  
 
== Parameters ==
 
== Parameters ==
Line 121: Line 123:
 
These fixed values are used within the model for the day scenario. A night scenario is also available, see [[#Variants|Variants]].
 
These fixed values are used within the model for the day scenario. A night scenario is also available, see [[#Variants|Variants]].
  
−
<math>
+
{| border="1" align="center" cellpadding="5" cellspacing="0"
−
\begin{array}{lcrr}
+
|- bgcolor=#c7c7c7
−
t_0                &=&    0.00, & s\\
+
! Symbol !! Value !! Unit !! Description
−
\dot{Q}_{airload}   &=& 3000.00, & \frac{J}{s} \\
+
|-
−
\dot{m}_{ref,const} &=&    0.20, & \frac{kg}{s} \\
+
| align=center | <math>\dot{Q}_{airload}</math> || align=right | 3000.00 || <math>\frac{J}{s}</math> || Disturbance, heat transfer from outside the display case
−
M_{goods}           &=&  200.00, & kg\\
+
|-
−
C_{p,goods}         &=& 1000.00, & \frac{J}{kg \cdot K} \\
+
| align=center | <math>\dot{m}_{ref,const}</math> || align=right | 0.20 || <math>\frac{kg}{s}</math> || Disturbance, constant mass flow of refrigerant
−
UA_{goods-air}     &=&  300.00, & \frac{J}{s \cdot K} \\
+
from unmodeled entities
−
M_{wall}           &=&  260.00, & kg\\
+
|-
−
C_{p,wall}         &=&  385.00, & \frac{J}{kg \cdot K} \\
+
| align=center | <math>M_{goods}</math> || align=right | 200.00 || <math>kg</math> || Mass of goods
−
UA_{air-wall}       &=&  500.00, & \frac{J}{s \cdot K} \\
+
|-
−
M_{air}             &=&  50.00, & kg\\
+
| align=center | <math>C_{p,goods}</math> || align=right | 1000.00 || <math>\frac{J}{kg \cdot K}</math> || Heat capacity of goods
−
C_{p,air}           &=& 1000.00, & \frac{J}{kg \cdot K} \\
+
|-
−
UA_{wall-ref,max}   &=& 4000.00, & \frac{J}{s \cdot K} \\
+
| align=center | <math>
−
\tau_{fill}         &=&  40.00, & s\\
+
UA_{goods-air} </math> || align=right | 300.00 || <math>\frac{J}{s \cdot K}</math> || Heat transfer coefficient between goods
−
T_{SH}             &=&  10.00, & K\\
+
and air
−
M_{ref,max}         &=&    1.00, & kg\\
+
|-
−
V_{suc}             &=&    5.00, & m^3\\
+
| align=center | <math>M_{wall} </math> || align=right | 260.00 || <math>kg</math> || Mass of evaporator wall
−
V_{sl}             &=&    0.08, & \frac{m^3}{s} \\
+
|-
−
\eta_{vol}         &=&    0.81, & -\\
+
| align=center | <math>C_{p,wall} </math> || align=right | 385.00 || <math>\frac{J}{kg \cdot K}</math> || Heat capacity of evaporator wall
−
 
+
|-
−
 
+
| align=center | <math>UA_{air-wall}</math> || align=right | 500.00 || <math>\frac{J}{s \cdot K}</math> || Heat transfer coefficient between air and
−
\end{array}
+
wall
−
</math>
+
|-
 +
| align=center | <math>M_{air}</math> || align=right | 50.00 || <math>kg</math> || Mass of air in display case
 +
|-
 +
| align=center | <math>C_{p,air}</math> || align=right | 1000.00 || <math>\frac{J}{kg \cdot K}</math> || Heat capacity of air
 +
|-
 +
| align=center | <math>UA_{wall-ref,max}</math> || align=right | 4000.00 || <math>\frac{J}{s \cdot K}</math> || Maximum heat transfer coefficient between
 +
refrigerant and evaporator wall
 +
|-
 +
| align=center | <math>\tau_{fill}</math> || align=right | 40.00 || <math>s</math> || Parameter describing the filling time of the
 +
evaporator under opened valve
 +
|-
 +
| align=center | <math>T_{SH}</math> || align=right | 10.00 || <math>K</math> || Superheat in the suction manifold
 +
|-
 +
| align=center | <math>M_{ref,max}</math> || align=right | 1.00 || <math>kg</math> || Maximum mass of refrigerant in evaporator
 +
|-
 +
| align=center | <math>V_{suc}</math> || align=right | 5.00 || <math>m^3</math> || Total volume of suction manifold
 +
|-
 +
| align=center | <math>V_{sl}</math> || align=right | 0.08 || <math>\frac{m^3}{s}</math> || Total displacement volume
 +
|-
 +
| align=center | <math>\eta_{vol}</math> || align=right | 0.81 || <math>-</math> || Volumetric efficiency
 +
|}
  
 
== Reference Solutions ==
 
== Reference Solutions ==
  
−
For the relaxed problem (we only demand <math>u_i(t) \in  [0,1]</math> instead of <math>u_i(t) \in  \{0,1\}</math> the optimal solution is 12072.45.
+
For the relaxed problem (we only demand <math>u_i(t) \in  [0,1]</math> instead of <math>u_i(t) \in  \{0,1\}</math>) the optimal solution is 12072.45.
−
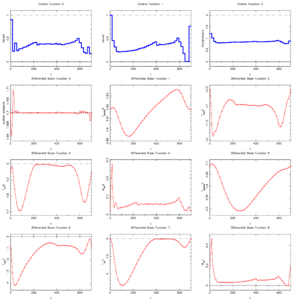
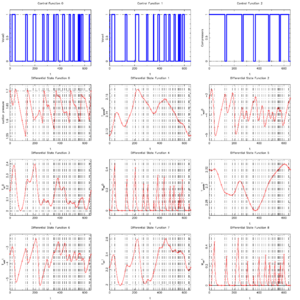
If we restrict ourselves to a solution with only integer controls we obtain the optimum objective value 12252.81.
+
The illustrated solution with integer controls has a (suboptimal) objective function value of 12252.81.
  
 
<gallery caption="Reference solution plots" widths="350px" heights="300px" perrow="2">
 
<gallery caption="Reference solution plots" widths="350px" heights="300px" perrow="2">
Line 158: Line 180:
 
== Source Code ==
 
== Source Code ==
  
−
=== C ===
+
Model descriptions are available in
−
 
+
−
The differential equations in C code:
+
−
<source lang="cpp">
+
−
// number of compressors
+
−
#define NVALVES 2
+
−
 
+
−
// constants
+
−
#define M_GOODS 200.0
+
−
#define C_P_GOODS 1000.0
+
−
#define UA_GOODS_AIR 300.0
+
−
#define M_WALL 260.0
+
−
#define C_P_WALL 385.0
+
−
#define UA_AIR_WALL 500.0
+
−
#define M_AIR 50.0
+
−
#define C_P_AIR 1000.0
+
−
#define UA_WALL_REF_MAX 4000.0
+
−
#define M_REF_MAX 1.0
+
−
#define TAU_FILL 40.0
+
−
#define T_SH 10.0
+
−
#define V_SUC 5.0
+
−
#define V_SL 0.08 // 2 display cases - 2 compressors
+
−
// #define V_SL 0.095 // 3 display cases - 3 compressors
+
−
#define ETA_VOL 0.81
+
−
 
+
−
// disturbances - day scenario
+
−
#define Q_AIRLOAD 3000.0
+
−
#define M_REF_CONST 0.2
+
−
 
+
−
// disturbances - night scenario
+
−
// #define Q_AIRLOAD 1800.0
+
−
// #define M_REF_CONST 0.0
+
−
 
+
−
double delta_h = (0.0217*xd[0]*xd[0] - 0.1704*xd[0] + 2.2988)*1e5;
+
−
double T_e = -4.3544*xd[0]*xd[0] + 29.224*xd[0] - 51.2005;
+
−
double rho_suc = 4.6073*xd[0] + 0.3798;
+
−
double rho_suc__P_suc = -0.0329*xd[0]*xd[0]*xd[0] + 0.2161*xd[0]*xd[0] - 0.4742*xd[0] + 5.4817;
+
−
double f = (0.0265*xd[0]*xd[0]*xd[0] -0.4346*xd[0]*xd[0] + 2.4923*xd[0] + 1.2189)*1e5;
+
−
 
+
−
double Q_goods_air[NVALVES];
+
−
double Q_air_wall[NVALVES];
+
−
double UA_wall_ref[NVALVES];
+
−
double Q_e[NVALVES];
+
−
double m[NVALVES];
+
−
 
+
−
double m_in_suc = 0.0;
+
−
 
+
−
int i;
+
−
 
+
−
for (i=0; i<NVALVES; i++){
+
−
    Q_goods_air[i] = UA_GOODS_AIR*(xd[1 + i*4] - xd[3 + i*4]);
+
−
    Q_air_wall[i] = UA_AIR_WALL*(xd[3 + i*4] - xd[2 + i*4]);
+
−
    UA_wall_ref[i] = UA_WALL_REF_MAX * xd[4 + 4*i]/M_REF_MAX;
+
−
    Q_e[i] = UA_wall_ref[i]*(xd[2 + 4*i] - T_e);
+
−
 
+
−
    m[i] = Q_e[i]/delta_h;
+
−
    m_in_suc += m[i];
+
−
}
+
−
 
+
−
double V_comp = 0.0;
+
−
double comp_scale = (double) 1.0/NCOMPS;
+
−
V_comp = comp_scale*u[NVALVES]*ETA_VOL*V_SL;
+
−
 
+
−
+
−
 
+
−
// suction pressure
+
−
rhs[0] = (m_in_suc + M_REF_CONST - V_comp*rho_suc) / (V_SUC*rho_suc__P_suc);
+
−
 
+
−
// for each display/valve
+
−
for (i=0; i<NVALVES; i++){
+
−
 
+
−
    // temperatures:
+
−
 
+
−
    // goods
+
−
    rhs[1 + i*4] = - Q_goods_air[i]/(M_GOODS*C_P_GOODS);
+
−
 
+
−
    // wall
+
−
    rhs[2 + i*4] = (Q_air_wall[i] - Q_e[i])/(M_WALL*C_P_WALL);
+
−
 
+
−
    // air
+
−
    rhs[3 + i*4] = ((Q_goods_air[i] + Q_AIRLOAD - Q_air_wall[i]) /(M_AIR*C_P_AIR));
+
  
−
    // mass of liquefied refrigerant:
+
* [[:Category:Muscod | Muscod code]] at [[Supermarket refrigeration system (Muscod)]]
−
    rhs[4 + i*4] = ((M_REF_MAX - xd[4 + 4*i])/TAU_FILL * u[i] - m[i] * (1 - u[i]));
+
* [[:Category:JModelica | JModelica code]] at [[Supermarket refrigeration system (JModelica)]]
−
}
+
−
</source>
+
  
 
== Variants ==
 
== Variants ==
Line 249: Line 189:
 
Since the compressors are parallel connected one can introduce a single control <math> u_2 \in \{0,1,2\}</math> instead of two equivalent controls. The same holds for scenarions with <math> n </math> parallel connected compressors.
 
Since the compressors are parallel connected one can introduce a single control <math> u_2 \in \{0,1,2\}</math> instead of two equivalent controls. The same holds for scenarions with <math> n </math> parallel connected compressors.
  
−
In the paper <bibref>Larsen2007</bibref> mentioned above, the problem was stated slightly different:
+
In the paper <bib id="Larsen2007" /> mentioned above, the problem was stated slightly different:
  
 
* The temperature constraints weren't hard bounds but there was a penalization term added to the objective function to minimize the violation of these constraints.
 
* The temperature constraints weren't hard bounds but there was a penalization term added to the objective function to minimize the violation of these constraints.
Line 277: Line 217:
  
 
== References ==
 
== References ==
−
<bibreferences/>
+
<biblist />
  
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
Line 284: Line 224:
 
[[Category:Chattering]]
 
[[Category:Chattering]]
 
[[Category:Periodic]]
 
[[Category:Periodic]]
 +
[[Category:Minimum energy]]

Latest revision as of 09:33, 27 July 2016

Supermarket refrigeration system
State dimension: 1
Differential states: 9
Discrete control functions: 3
Path constraints: 7
Interior point equalities: 9


The supermarket refrigeration system problem is based on a model describing a refrigeration system with 2 parallel connected compressors (called a compressor rack) which only can be controlled stepwise (each single compressor can be turned on or off) and 2 open refrigerated display cases containing goods needed to be refrigerated. Each display case is connected to the refrigeration circuit through an expansion valve which also can only be closed or opened. This valve controls the flow of refrigerant into the evaporator, where it absorbs heat from the surrounding air. The refrigerated air then creates the well-known air-curtain at the front of the display case.

The air temperatures surrounding the goods in each display case are modeled by one differential state each. These states have to be bounded, so that the goods are properly refrigerated.

The model was published by Larsen et. al. in 2007 [Larsen2007]Author: Larsen, L.F.S.; Izadi-Zamanabadi, R.; Wisniewski, R.; Sonntag, C.
Institution: Technical report for the HYCON NoE.
Note: http://www.bci.tu-dortmund.de/ast/hycon4b/index.php
Title: Supermarket Refrigeration Systems -- A benchmark for the optimal control of hybrid systems
Year: 2007
Link to Google Scholar. The main goal is to control the refirgeration system energy-optimal. The problem was set up as a benchmark problem for MIOCPs.

The mathematical equations form an ODE model. The initial values of the differential states are not fixed but periodicity of the whole process is required.

The optimal integer control function shows chattering behavior, making the supermarket refrigeration system problem a candidate for benchmarking of algorithms.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

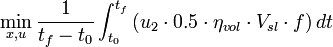
\min_{x,u} \frac {1}{t_f - t_0}\int_{t_0}^{t_f} \left( u_2 \cdot 0.5 \cdot \eta_{vol} \cdot V_{sl} \cdot f \right) dt

\begin{array}{llcl} \displaystyle \mbox{s.t.} & \dot{x_0} &=& \dfrac{1}{V_{suc} \cdot \frac{d\rho_{suc}}{dP_{suc}}(x_0)} \cdot \bigg[ \left(\dfrac{UA_{wall-ref, max}}{M_{ref, max} \cdot \Delta h_{lg}(x_0)}\right) \Big( x_4 \big( x_2 - T_e(x_0) \big)\\ & && + \, x_8 \big( x_6 - T_e(x_0) \big) \Big) + \, M_{ref,const} - \eta_{vol} \cdot V_{sl} \cdot 0.5 \, u_2 \rho_{suc}(x_0) \bigg] \\ &\dot{x_1} &=& - \dfrac{ UA_{goods-air} \left( x_1 - x_3 \right) }{ M_{goods} \cdot C_{p,goods} } \\ &\dot{x_2} &=& \dfrac{ UA_{air-wall} \left( x_3-x_2 \right) - \dfrac{UA_{wall-ref,max}}{M_{ref,max}} \, x_4 \big( x_2 - T_e(x_0) \big) }{ M_{wall} \cdot C_{p,wall} } \\ [2.5ex] &\dot{x_3} &=& \dfrac{ UA_{goods-air} \left( x_1-x_3 \right) + \dot{Q}_{airload} - UA_{air-wall} \, (x_3-x_2) }{ M_{air} \cdot C_{p,air} } \\ [2.5ex] &\dot{x_4} &=& \left(\dfrac{M_{ref,max} - x_4}{\tau_{fill}} \right) u_0 - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \, x_4 \big( x_2 - T_e(x_0) \big) \right) (1-u_0) \\ \\ &\dot{x_5} &=& - \dfrac{ UA_{goods-air} \left( x_5 - x_7 \right) }{ M_{goods} \cdot C_{p,goods} } \\ &\dot{x_6} &=& \dfrac{ UA_{air-wall} \left( x_7-x_6 \right) - \dfrac{UA_{wall-ref,max}}{M_{ref,max}} \, x_8 \big( x_6 - T_e(x_0) \big) }{ M_{wall} \cdot C_{p,wall} } \\ [2.5ex] &\dot{x_7} &=& \dfrac{ UA_{goods-air} \left( x_5-x_7 \right) + \dot{Q}_{airload} - UA_{air-wall} \, (x_7-x_6) }{ M_{air} \cdot C_{p,air} } \\ [2.5ex] &\dot{x_8} &=& \left(\dfrac{M_{ref,max} - x_8}{\tau_{fill}} \right) u_1 - \left( \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} \, x_8 \big( x_6 - T_e(x_0) \big) \right) (1-u_1) \\ [4ex] & x_3 &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\ & x_3 &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\ & x_7 &\geq& 2.0 \quad \forall t \in [t_0, t_f],\\ & x_7 &\leq& 5.0 \quad \forall t \in [t_0, t_f],\\ & x_0 &\leq& 1.7 \quad \forall t \in [t_0, t_f], \\ & x_i(t_0) &=& free \quad \forall i \in \{0,\dots, 8\}, \\ & x_i(t_f) &=& x_i(t_0) \quad \forall i \in \{0,\dots, 8\}, \\ & u_i(t) &\in& \{0, 1\} \quad \forall i \in \{0,\dots, 2\}, \\ & t_f &\in& [ 650, 750 ]. \end{array}


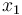Here the differential state x_0 describes the suction pressure in the suction manifold (in bar). The next three states model temperatures in the first display case (in °C). x_1 is the goods' temperature, 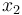x_2 the one of the evaporator wall and 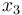x_3 the air temperature surrounding the goods. 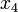x_4 then models the mass of the liquefied refrigerant in the evaporator (in kg).

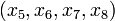(x_5, x_6, x_7, x_8) describe the corresponding states in the second display case.

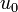u_0 describes the inlet valve of the first display case, 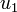u_1 respectively the valve of the second display case. 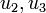u_2, u_3 denote the activity of a single compressor.

The following polynomial functions are used in the model description originating from interpolations:

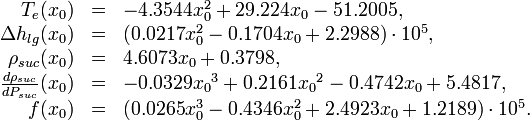
\begin{array}{rcl} T_e(x_0) &=& -4.3544 x_0^2 + 29.224 x_0 - 51.2005,\\ \Delta h_{lg}(x_0) &=& (0.0217 x_0^2 - 0.1704 x_0 + 2.2988)\cdot 10^5, \\ \rho_{suc}(x_0) &=& 4.6073 x_0 + 0.3798, \\ \frac{d\rho_{suc}}{dP_{suc}}(x_0) &=& -0.0329 {x_0}^3 + 0.2161 {x_0}^2 - 0.4742 x_0 + 5.4817,\\ f(x_0) &=& (0.0265 x_0^3 - 0.4346 x_0^2 + 2.4923 x_0 + 1.2189) \cdot 10^5. \end{array}

Parameters

These fixed values are used within the model for the day scenario. A night scenario is also available, see Variants.

Symbol Value Unit Description
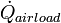\dot{Q}_{airload} 3000.00 \frac{J}{s} Disturbance, heat transfer from outside the display case
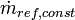\dot{m}_{ref,const} 0.20 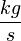\frac{kg}{s} Disturbance, constant mass flow of refrigerant

from unmodeled entities

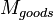M_{goods} 200.00 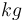kg Mass of goods
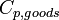C_{p,goods} 1000.00 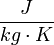\frac{J}{kg \cdot K} Heat capacity of goods
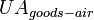UA_{goods-air} 300.00 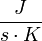\frac{J}{s \cdot K} Heat transfer coefficient between goods

and air

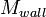M_{wall} 260.00 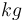kg Mass of evaporator wall
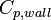C_{p,wall} 385.00 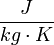\frac{J}{kg \cdot K} Heat capacity of evaporator wall
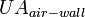UA_{air-wall} 500.00 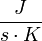\frac{J}{s \cdot K} Heat transfer coefficient between air and

wall

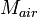M_{air} 50.00 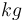kg Mass of air in display case
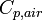C_{p,air} 1000.00 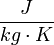\frac{J}{kg \cdot K} Heat capacity of air
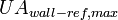UA_{wall-ref,max} 4000.00 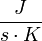\frac{J}{s \cdot K} Maximum heat transfer coefficient between

refrigerant and evaporator wall

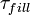\tau_{fill} 40.00 s Parameter describing the filling time of the

evaporator under opened valve

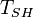T_{SH} 10.00 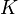K Superheat in the suction manifold
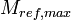M_{ref,max} 1.00 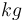kg Maximum mass of refrigerant in evaporator
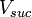V_{suc} 5.00 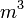m^3 Total volume of suction manifold
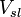V_{sl} 0.08 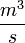\frac{m^3}{s} Total displacement volume
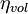\eta_{vol} 0.81 - Volumetric efficiency

Reference Solutions

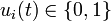For the relaxed problem (we only demand u_i(t) \in [0,1] instead of u_i(t) \in \{0,1\}) the optimal solution is 12072.45. The illustrated solution with integer controls has a (suboptimal) objective function value of 12252.81.

  • Reference solution plots

  • Optimal relaxed control.

  • Optimal integer control.

Source Code

Model descriptions are available in

Variants

Since the compressors are parallel connected one can introduce a single control 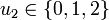u_2 \in \{0,1,2\} instead of two equivalent controls. The same holds for scenarions with n parallel connected compressors.

In the paper [Larsen2007]Author: Larsen, L.F.S.; Izadi-Zamanabadi, R.; Wisniewski, R.; Sonntag, C.
Institution: Technical report for the HYCON NoE.
Note: http://www.bci.tu-dortmund.de/ast/hycon4b/index.php
Title: Supermarket Refrigeration Systems -- A benchmark for the optimal control of hybrid systems
Year: 2007
Link to Google Scholar mentioned above, the problem was stated slightly different:

  • The temperature constraints weren't hard bounds but there was a penalization term added to the objective function to minimize the violation of these constraints.
  • The differential equation for the mass of the refrigerant had another switch, if the valve (e.g. u_0) is closed. It was formulated this way:

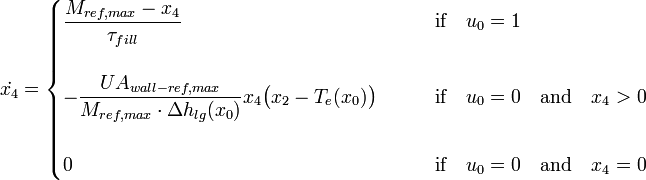
\dot{x_4} = \begin{cases} \dfrac{M_{ref,max} - x_4}{\tau_{fill}} & \qquad \text{if} \quad u_0 = 1 \\ \\ - \dfrac{UA_{wall-ref,max}}{M_{ref,max} \cdot \Delta h_{lg}(x_0)} x_4 \big( x_2 - T_e(x_0) \big) & \qquad \text{if} \quad u_0 = 0 \quad \text{and}\quad x_4 > 0 \\ \\ 0 & \qquad \text{if} \quad u_0 = 0 \quad \text{and} \quad x_4 = 0 \end{cases}

This additional switch is redundant because the mass itself is a factor on the right hand side and so the complete right hand side is 0 if 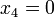x_4 = 0.

  • A night scenario with two different parameters was given. At night the following parameters change their value:

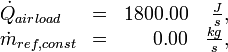
\begin{array}{lcrr} \dot{Q}_{airload} &=& 1800.00 & \frac{J}{s}, \\ \dot{m}_{ref,const} &=& 0.00 & \frac{kg}{s}, \\ \end{array}

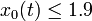Additionally the constraint on the suction pressure x_0(t) is softened to x_0(t) \leq 1.9.

  • No periodicity was required but the solution on a fixed time horizon 4 hours - 2 in day scenario and 2 in night scenario - with 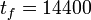t_f = 14400 was asked.
  • The number of compressors and display cases is not fixed. Larsen also proposed the problem with 3 compressors and 3 display cases. This leads to a change in the compressor rack's preformance to 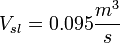V_{sl} = 0.095 \frac{m^3}{s}. Unfortunately this constant is only given for these two cases although Larsen proposed scenarios with more compressors and display cases.

References

There were no citations found in the article.

Retrieved from "https://mintoc.de/index.php?title=Supermarket_refrigeration_system&oldid=2120"