Difference between revisions of "Marine population dynamics problem"
From mintOC
FelixMueller (Talk | contribs) (Created page with "{{Dimensions |nd = 1 |nx = n_2 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... -->The Marine population dynamics problem estima...") |
FelixMueller (Talk | contribs) (→Mathematical formulation) |
||
| Line 15: | Line 15: | ||
<math> | <math> | ||
\begin{array}{llcl} | \begin{array}{llcl} | ||
| − | \displaystyle \min_{ | + | \displaystyle \min_{g, m} & \sum\limits_{j=1}^{n_m} &&||y(\tau_j; g, m) - z_j||^2 \\[1.5ex] |
\mbox{s.t.} | \mbox{s.t.} | ||
| − | & \dot{y}_j & = & g_{j-1} y_{j-1} - (m_j + g_j) y_j \ | + | & \dot{y}_j & = & g_{j-1} y_{j-1} - (m_j + g_j) y_j \qquad \forall j \in 1, ..., n_s,\\ |
& g_j, m_j &\in& [0,1]. | & g_j, m_j &\in& [0,1]. | ||
\end{array} | \end{array} | ||
Revision as of 18:59, 5 May 2016
| Marine population dynamics problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | n_2 |
The Marine population dynamics problem estimates growth and mortality rates of a marine species at each stage (for example ages or development stage) given the population as a function of time.( Problem taken from the COPS library)
Mathematical formulation
The problem is given by
![\begin{array}{llcl}
\displaystyle \min_{g, m} & \sum\limits_{j=1}^{n_m} &&||y(\tau_j; g, m) - z_j||^2 \\[1.5ex]
\mbox{s.t.}
& \dot{y}_j & = & g_{j-1} y_{j-1} - (m_j + g_j) y_j \qquad \forall j \in 1, ..., n_s,\\
& g_j, m_j &\in& [0,1].
\end{array}](https://mintoc.de/images/math/b/a/6/ba686bce5cfd80ce0f888915706e2d57.png)
where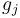 
and 
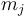are the growth and mortality rates at stage 
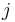respectively and the initial conditions are unknown.
The error between computed and observed data is minimized.
Parameters
There are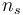 
stages and 
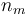timepoints at which the error is minimized.
Source Code
Model descriptions are available in
