Difference between revisions of "LinearMetabolic"
(Created page with "{{Dimensions |nd = 1 |nx = 4 |nw = 1 |nc = 2 |nri = 2 |nre = 5 }}<!-- Do not insert line break here or Dimensions Box moves up in the...") |
m (Tsiantis reference) |
||
| Line 13: | Line 13: | ||
The '''Linear Metabolic problem''' is a generalized inverse optimal control problem. It tries to identify an a priori unknown objective function from data. The control unction <math> u(t) </math> is ... | The '''Linear Metabolic problem''' is a generalized inverse optimal control problem. It tries to identify an a priori unknown objective function from data. The control unction <math> u(t) </math> is ... | ||
| − | The problem is discussed in detail in <bib id=" | + | The problem is discussed in detail in <bib id="Tsiantis2018" />. |
== Mathematical formulation == | == Mathematical formulation == | ||
Revision as of 14:41, 19 October 2023
| LinearMetabolic | |
|---|---|
| State dimension: | 1 |
| Differential states: | 4 |
| Discrete control functions: | 1 |
| Path constraints: | 2 |
| Interior point inequalities: | 2 |
| Interior point equalities: | 5 |
Under construction...
The Linear Metabolic problem is a generalized inverse optimal control problem. It tries to identify an a priori unknown objective function from data. The control unction 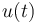 is ...
is ...
The problem is discussed in detail in [Tsiantis2018]Author: Tsiantis, Nikolaos; Balsa-Canto, Eva; Banga, Julio R
Journal: Bioinformatics
Number: 14
Pages: 2433-2440
Title: Optimality and identification of dynamic models in systems biology: an inverse optimal control framework
Volume: 34
Year: 2018 .
.
Contents
[hide]Mathematical formulation
The mixed-integer optimal control problem is given by
![\begin{array}{llclr}
\displaystyle \min_{x, u} & x_3(t_f) \\[1.5ex]
\mbox{s.t.}
& \dot{x}_0 & = & (V_{alim} u - R_m x_0 - K_m x_1) / L_m, \\
& \dot{x}_1 & = & \frac{K_r^2}{Mr^2} (K_m x_0 - \frac{r}{K_r} ( M g K_f + \frac{1}{2} \rho S C_x \frac{r^2}{K_r^2} x_1^2)), \\
& \dot{x}_2 & = & \frac{r}{K_r} x_1, \\
& \dot{x}_3 & = & V_{alim} u x_0 + R_{bat} x_0^2, \\[1.5ex]
& x(t_0) &=& (0,0,0,0)^T, \\
& x(t_f) & \in & \mathcal{T} \subseteq \mathbb{R}^4,\\
& x_0(t) & \in & [-i_{max}, i_{max}], \\
& u(t) &\in& \{-1, 1\}.
\end{array}](https://mintoc.de/images/math/f/8/1/f81a52adee4116324d4656c5e4256abb.png)
Here the four differential states stand for the electrical current (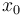 ), the angular velocity (
), the angular velocity (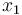 ), the position of the car (
), the position of the car (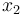 ), and the consumed energy (
), and the consumed energy (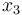 ). The objective function
). The objective function 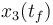 is just a reformulation of the Lagrange-type objective function tracking the used energy over time.
is just a reformulation of the Lagrange-type objective function tracking the used energy over time.
Parameters
These fixed values are used within the model.
| Name | Symbol | Value | Unit |
| Coefficient of reduction | 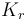
|
10 | [-] |
| Air density | 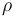
|
1.293 | 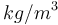
|
| Aerodynamic coefficient | 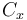
|
0.4 | [-] |
| Area in the front of the vehicle | 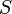
|
2 | 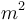
|
| Radius of the wheel | 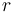
|
0.33 | 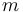
|
| Constant representing the friction of the wheels on the road | 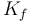
|
0.03 | [-] |
| Coefficient of the motor torque | 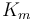
|
0.27 | [-] |
| Inductor resistance | 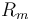
|
0.03 | 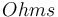
|
| inductance of the rotor | 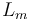
|
0.05 | [-] |
| Mass | 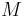
|
250 | 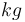
|
| Gravity constant | 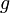
|
9,81 | [-] |
| Battery voltage | 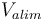
|
150 | 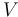
|
| Resistance of the battery | 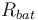
|
0.05 | 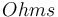
|
Reference Solutions
We look at the particular instance of our problem with 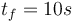 and target set
and target set 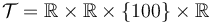 , in which the car needs to cover 100m in 10s.
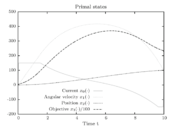
Figure 1 shows a plot of the differential states of the optimal trajectory of the relaxed problem (i.e.
, in which the car needs to cover 100m in 10s.
Figure 1 shows a plot of the differential states of the optimal trajectory of the relaxed problem (i.e. ![u \in [-1,1]](https://mintoc.de/images/math/7/7/e/77ebca4c196d281ab127d484baf6bd92.png) instead of
instead of 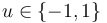 ) for
) for 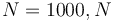 being the number of time discretization points. The current
being the number of time discretization points. The current 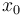 increases to its maximal value of 150A, stays there for a certain time, decreases on its minimal value of -150A, stays on this value and eventually increases slightly. This behavior corresponds to the different arcs bang, path-constrained, singular, path-constrained, bang and can be observed also in Figure 2. It shows the corresponding switching function and the optimal control. Note that the plots show data from the solution with the indirect approach.
increases to its maximal value of 150A, stays there for a certain time, decreases on its minimal value of -150A, stays on this value and eventually increases slightly. This behavior corresponds to the different arcs bang, path-constrained, singular, path-constrained, bang and can be observed also in Figure 2. It shows the corresponding switching function and the optimal control. Note that the plots show data from the solution with the indirect approach.
Applying the sum up rounding strategy results in an integer-feasible chattering solution.
The resulting primal states are shown in Figure 3. One observes the high-frequency zig-zagging of the current 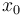 that results from the fast switches in the control.
that results from the fast switches in the control.
The direct and indirect approaches are local optimization techniques and only provide upper bounds for the relaxed problem and hence for the original problem. Here the indirect solution of the relaxed problem gives us a bound of 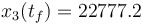 .
.
- Reference solution plots
Source Code
Model descriptions are available in
Variants
There are several alternative formulations and variants of the above problem, in particular
- fixed final velocity,
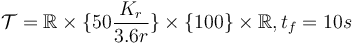
- bounded velocity,
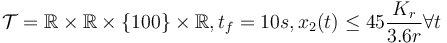
- fixed final velocity, bounded velocity, longer time horizon,
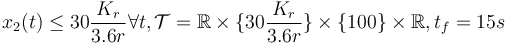 .
.
References
| [Sager2015] | Sager, S.; M. Claeys; F. Messine (2015): Efficient upper and lower bounds for global mixed-integer optimal control. Journal of Global Optimization, 61, 721--743 |  |
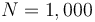 .
.

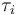 where transitions between different kinds of arcs occur.
where transitions between different kinds of arcs occur.

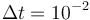 .
.