Difference between revisions of "Category:ODE model"
m (Added extensions) |
m (Added Outer convexification) |
||
| Line 34: | Line 34: | ||
* The dynamics might be [[:Category:Unstable | unstable]]. | * The dynamics might be [[:Category:Unstable | unstable]]. | ||
* There might be an underlying [[:Category:Network topology | network topology]]. | * There might be an underlying [[:Category:Network topology | network topology]]. | ||
| + | * The integer control functions might have been (re)formulated by means of an [[:Category:Outer convexification|outer convexification]]. | ||
Note that a Lagrange term <math>\int_{t_0}^{t_f} L( x(t), u(t), v(t), q, \rho) \; \mathrm{d} t</math> can be transformed into a Mayer-type objective functional. | Note that a Lagrange term <math>\int_{t_0}^{t_f} L( x(t), u(t), v(t), q, \rho) \; \mathrm{d} t</math> can be transformed into a Mayer-type objective functional. | ||
[[Category:Model characterization]] | [[Category:Model characterization]] | ||
Latest revision as of 12:02, 20 November 2010
This category includes all problems constrained by the solution of ordinary differential equations (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only (typically time) are present in the model equations for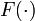 
.
The mixed-integer optimal control problem is of the form
![\begin{array}{llcl}
\displaystyle \min_{x(\cdot), u(\cdot), v(\cdot), q, \rho} & \phi(x(t_f), q, \rho) \\[1.5ex]
\mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t), q, \rho), \\
& 0 &\le& c(x(t),u(t),v(t), q, \rho), \\[1.5ex]
& 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\
& 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\[1.5ex]
& v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \},\\
& \rho &\in& \Rho := \{\rho^1, \rho^2, \dots, \rho^{n_\Rho} \},
\end{array}](https://mintoc.de/images/math/c/2/e/c2ea6ba320c6ca71260f7eeb98105969.png)
for ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png)
almost everywhere.
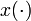denotes the differential states,
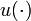denotes the continuous control functions,
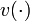denotes the integer control functions,
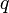denotes the continuous (constant-in-time) control values,
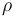denotes the integer (constant-in-time) control values.
The multipoint constraints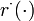 
are defined on a time grid 
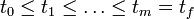. The Mayer term functional 
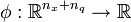, the path- and control constraints 
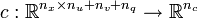and the constraint functions 
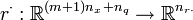are assumed to be sufficiently often differentiable.
The equality constraints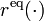 
will often fix the initial values, i.e., 
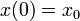, or impose a periodicity constraint.
Extensions
- For some problems the functions may as well depend explicitely on the time
. - The differential equations might depend on state-dependent switches.
- The variables may include boolean variables.
- The underlying process might be a multistage process.
- The dynamics might be unstable.
- There might be an underlying network topology.
- The integer control functions might have been (re)formulated by means of an outer convexification.
Note that a Lagrange term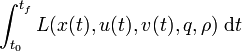 
can be transformed into a Mayer-type objective functional.
Pages in category "ODE model"
The following 52 pages are in this category, out of 52 total.
