F-8 aircraft

From mintOC
Revision as of 09:44, 10 August 2009 by PaulineBoizet (Talk | contribs) (→‎Optimica)

Jump to: navigation, search
F-8 aircraft
State dimension: 1
Differential states: 3
Discrete control functions: 1
Interior point equalities: 6


The F-8 aircraft control problem is based on a very simple aircraft model. The control problem was introduced by Kaya and Noakes and aims at controlling an aircraft in a time-optimal way from an initial state to a terminal state.

The mathematical equations form a small-scale ODE model. The interior point equality conditions fix both initial and terminal values of the differential states.

The optimal, relaxed control function shows bang bang behavior. The problem is furthermore interesting as it should be reformulated equivalently.

Mathematical formulation

For t \in [0, T] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& - 20.967 \; w + 6.265 \; x_0^2 \; w + 46 \; x_0 \; w^2 + 61.4 \; w^3 \\ & x(0) &=& (0.4655,0,0)^T, \\ & x(T) &=& (0,0,0)^T, \\ & w(t) &\in& \{-0.05236,0.05236\}. \end{array}

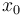x_0 is the angle of attack in radians, 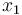x_1 is the pitch angle, 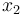x_2 is the pitch rate in rad/s, and the control function 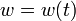w = w(t) is the tail deflection angle in radians. This model goes back to Garrard<bibref>Garrard1977</bibref>.

In the control problem, both initial and terminal values of the differential states are fixed.

Reformulation

The control w(t) is restricted to take values from a finite set only. Hence, the control problem can be reformulated equivalently to

\begin{array}{llcl} \displaystyle \min_{x, w, T} & T \\[1.5ex] \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& - \left( 0.215 \; \xi - 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 - 0.63 \; \xi^3 \right) \; w \\ &&& - \left( - 0.215 \; \xi + 0.28 \; x_0^2 \; \xi - 0.47 \; x_0 \; \xi^2 + 0.63 \; \xi^3 \right) \; (1 - w) \\ & &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& + 0.215 \; \xi - 0.28 \; x_0^2 \; \xi + 0.47 \; x_0 \; \xi^2 - 0.63 \; \xi^3 \\ &&& - \left( 0.215 \; \xi - 0.28 \; x_0^2 \; \xi - 0.63 \; \xi^3 \right) \; 2 w \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& - \left( 20.967 \; \xi - 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 - 61.4 \; \xi^3 \right) \; w \\ &&& - \left( - 20.967 \; \xi + 6.265 \; x_0^2 \; \xi -46 \; x_0 \; \xi^2 + 61.4 \; \xi^3 \right) \; (1 - w) \\ & &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& + 20.967 \; \xi - 6.265 \; x_0^2 \; \xi + 46 \; x_0 \; \xi^2 - 61.4 \; \xi^3 \\ &&& - \left( 20.967 \; \xi - 6.265 \; x_0^2 \; \xi - 61.4 \; \xi^3 \right) \; 2 w \\ & x(0) &=& (0.4655,0,0)^T, \\ & x(T) &=& (0,0,0)^T, \\ & w(t) &\in& \{0,1\}, \end{array}

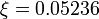with \xi = 0.05236. Note that there is a bijection between optimal solutions of the two problems.

Reference solutions

We provide here a comparison of different solutions reported in the literature. The numbers show the respective lengths 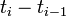t_i - t_{i-1} of the switching arcs with the value of 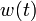w(t) on the upper or lower bound (given in the second column). Claim denotes what is stated in the respective publication, Simulation shows values obtained by a simulation with a Runge-Kutta-Fehlberg method of 4th/5th order and an integration tolerance of 10^{-8}.

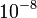Arc w(t) Lee et al.<bibref>Lee1997a</bibref> Kaya<bibref>Kaya2003</bibref> Sager<bibref>Sager2005</bibref> Schlueter/ Gerdts Sager
1 1 0.00000 0.10292 0.10235 0.0 1.13492
2 0 2.18800 1.92793 1.92812 0.608750 0.34703
3 1 0.16400 0.16687 0.16645 3.136514 1.60721
4 0 2.88100 2.74338 2.73071 0.654550 0.69169
5 1 0.33000 0.32992 0.32994 0.0 0.0
6 0 0.47200 0.47116 0.47107 0.0 0.0
Claim: Infeasibility - 1.00E-10 7.30E-06 5.90E-06 3.29169e-06 2.21723e-07
Claim: Objective - 6.03500 5.74217 5.72864 4.39981 3.78086
Simulation: Infeasibility - 1.75E-03 1.64E-03 5.90E-06 3.29169e-06 2.21723e-07
Simulation: Objective - 6.03500 5.74218 5.72864 4.39981 3.78086

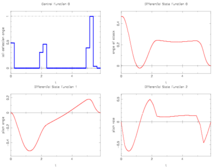
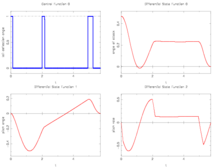
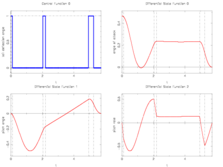
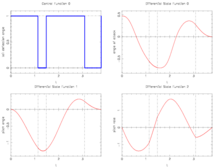
The best known optimal objective value of this problem given is given by 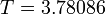T = 3.78086. The corresponding solution is shown in the rightmost plot. The solution of bang-bang type switches three times, starting with w(t) = 1.

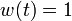  • Reference solution plots

  • Locally optimal relaxed control on a coarse control discretization grid and corresponding differential states.

  • Locally optimal relaxed control on a fine, adaptively chosen control discretization grid and corresponding differential states.

  • Integer control and corresponding differential states from Sager<bibref>Sager2005</bibref>.

  • Integer control and corresponding differential states from Schlueter/ Gerdts solution.

  • Best known integer control and corresponding differential states from Sager solution.

Source Code

C

The differential equations in C code: 

  double x1 = xd[0];
  double x2 = xd[1];
  double x3 = xd[2];
 
#ifdef CONVEXIFIED
  double xi = 0.05236;
 
  rhs[0] = -0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2 -x1*x1*x3 + 3.846*x1*x1*x1
	         + 0.215*xi - 0.28*x1*x1*xi + 0.47*x1*xi*xi - 0.63*xi*xi*xi
	         - 2*u[0] * ( 0.215*xi - 0.28*x1*x1*xi - 0.63*xi*xi*xi );
  rhs[1] = x3;
  rhs[2] = - 4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
	         + 20.967*xi - 6.265*x1*x1*xi + 46*x1*xi*xi - 61.4*xi*xi*xi
	         - 2*u[0] * ( 20.967*xi - 6.265*x1*x1*xi - 61.4*xi*xi*xi );
#else
  double u_ = -0.05236 + u[0]*2.0*0.05236;
 
  rhs[0] = -0.877*x1 + x3 - 0.088*x1*x3 + 0.47*x1*x1 - 0.019*x2*x2
           -x1*x1*x3 + 3.846*x1*x1*x1 - 0.215*u_ + 0.28*x1*x1*u_ + 0.47*x1*u_*u_ + 0.63*u_*u_*u_;
  rhs[1] = x3;
  rhs[2] = -4.208*x1 - 0.396*x3 - 0.47*x1*x1 - 3.564*x1*x1*x1
           - 20.967*u_ + 6.265*x1*x1*u_ + 46*x1*u_*u_ + 61.4*u_*u_*u_;
#endif

Optimica

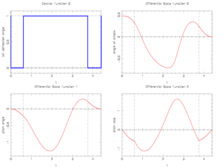
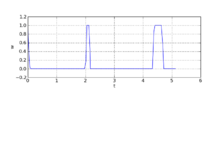
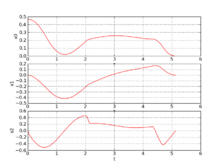
Model description in Optimica.Solver=Ipopt Objective  : 5.12799232 infeasibility : 6.2235588037251599e-10 

package F8_aircraft_pack
 
  optimization F8_aircraft_Opt (objective = tf,
                         startTime = 0,
                         finalTime = 1)
 
    // The time is scaled so that the new
    // time variable, call it \tau,
    // is related to the original time,
    // call it t as \tau=tf*t where tf
    // is a parameter to be minimized 
    // subject to the dynamics
    // \dot x = tf*f(x,w)
 
    // Parameters
    parameter Real tf(free=true,min=0.1);
    parameter Real ksi=0.05236;
 
    // The states
    Real x0(start=0.4655); //angle of attack
    Real x1(start=0); //pitch angle
    Real x2(start=0); //pitch rate
 
    // The control signal
    input Real  w(min=0,max=1);
 
  equation
 
    der(x0)= tf*(-0.877*x0 + x2 - 0.088*x0*x2 + 0.47*x0^2 - 0.019*x1^2 -x0^2*x2 + 3.846*x0^3
           -(0.215*ksi -0.28*x0^2*ksi -0.47*x0*ksi^2 - 0.63*ksi^3)*w
           -(-0.215*ksi + 0.28*x0^2 -0.47*x0*ksi^2 + 0.63*ksi^3)*(1-w));
    der(x1) = tf*x2;
    der(x2) = tf*(-4.208*x0 - 0.396*x2 - 0.47*x0^2 - 3.564*x0^3
              +20.967*ksi - 6.265*x0^2*ksi + 46*x0*ksi^2 - 61.4*ksi^3
              -(20.967*ksi - 6.265*x0^2*ksi - 61.4*ksi^3)*2*w);
  constraint
    x0(finalTime)=0;
    x1(finalTime)=0;
    x2(finalTime)=0;
 
  end F8_aircraft_Opt;
 
end F8_aircraft_pack;
  • Obtained solution plots

  • .

  • .

Variants

Miscellaneous and Further Reading

See <bibref>Kaya2003</bibref> and <bibref>Sager2005</bibref> for details.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=F-8_aircraft&oldid=501"