Category:Gekko
The GEKKO Python package<ref>Template:Cite journal</ref> solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (IPOPT, APOPT, BPOPT, SNOPT, MINOS). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation.
pip install gekko
GEKKO works on all platforms (Windows, MacOS, Linux, ARM processors) and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There is a Windows and Linux option to solve without an Internet connection. GEKKO is an extension of the APMonitor Optimization Suite but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71<ref>W. Hock and K. Schittkowski, Test Examples for Nonlinear Programming Codes, Lecture Notes in Economics and Mathematical Systems, Vol. 187, Springer 1981.</ref> used to test the performance of nonlinear programming solvers. This particular optimization problem has an objective function 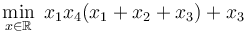 and subject to the inequality constraint
and subject to the inequality constraint 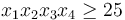 and equality constraint
and equality constraint 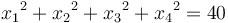 . The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are
. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are 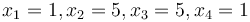 . This optimization problem is solved with GEKKO as shown below.
. This optimization problem is solved with GEKKO as shown below.
from gekko import GEKKO m = GEKKO() # Initialize gekko # Initialize variables x1 = m.Var(value=1,lb=1,ub=5) x2 = m.Var(value=5,lb=1,ub=5) x3 = m.Var(value=5,lb=1,ub=5) x4 = m.Var(value=1,lb=1,ub=5) # Equations m.Equation(x1*x2*x3*x4>=25) m.Equation(x1**2+x2**2+x3**2+x4**2==40) m.Obj(x1*x4*(x1+x2+x3)+x3) # Objective m.solve(disp=False) # Solve print('x1: ' + str(x1.value)) print('x2: ' + str(x2.value)) print('x3: ' + str(x3.value)) print('x4: ' + str(x4.value)) print('Objective: ' + str(m.options.objfcnval))
Applications of GEKKO
Applications include cogeneration (power and heat)<ref>Template:Cite journal</ref>, drilling automation<ref>Template:Cite journal</ref>, severe slugging control<ref>Template:Cite journal</ref>, solar thermal energy production<ref>Template:Cite journal</ref>, solid oxide fuel cells<ref>Template:Cite journal</ref><ref>Template:Cite journal</ref>, flow assurance <ref>Template:Cite journal</ref>, Enhanced oil recovery <ref>Template:Cite journal</ref>, Essential oil extraction<ref>Template:Cite journal</ref>, and Unmanned Aerial Vehicles (UAVs)<ref>Template:Cite journal</ref>. There are many other references to APMonitor and GEKKO as a sample of the types of applications that can be solved. GEKKO is developed from the National Science Foundation (NSF) research grant #1547110 <ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref><ref>Template:Cite journal</ref> and is detailed in a Special Issue collection on combined scheduling and control<ref>Template:Cite journal</ref>. Other notable mentions of GEKKO are the listing in the Decision Tree for Optimization Software<ref>Template:Cite web</ref>, added support for APOPT and BPOPT solvers<ref>Template:Cite web</ref>, projects reports of the online Dynamic Optimization course from international participants<ref>Template:Cite web</ref>. GEKKO is a topic in online forums where users are solving optimization and optimal control problems<ref>Template:Cite web</ref><ref>Template:Cite web</ref>. GEKKO is used for advanced control in the Temperature Control Lab (TCLab)<ref>Template:Cite web</ref> for process control education at 20 universities<ref>Template:Cite web</ref><ref>Template:Cite web</ref><ref>Template:Cite web</ref><ref>Template:Cite web</ref>.
References
External links
- GEKKO Documentation
- GEKKO Source Code
- GEKKO on PyPI for Python pip install
- GEKKO is open-source product of National Science Foundation (NSF) research grant 1547110
- References to APMonitor and GEKKO in the literature
- 18 examples of GEKKO: machine learning, optimal control, data regression
Pages in category "Gekko"
The following 6 pages are in this category, out of 6 total.