Source Inversion (FEniCS/Casadi)
This page contains a discretized version of the mixed integer PDE constrained optimization problem Source Inversion in CasADi 2.4.3 format. The weak version of the problem was discretized using finite element methods (via FEniCS) using first-degree Lagrangian elements on an equidistant mesh with 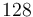cells.
CasADi
from dolfin import *
import math
import numpy
import scipy, scipy.sparse
import casadi
# Simple Branch and Bound solver
def solve_bnb(solver, root, integers):
# Initialize the node queue
Q = [(numpy.inf, root)]
# Global solution data
x_opt = None
f_opt = numpy.inf
# Continuous solution data
x0 = None
f0 = numpy.inf
# Main loop
seqnum = 0
while Q:
seqnum += 1
# Extract node with lowest lower bound and check if fathoming is necessary
# (should not happen)
node = Q.pop()
if f_opt < numpy.inf and node[0] >= f_opt:
print "Node %4d (%4d left): %9g >= %9g - PRE-FATHOM" % (seqnum, len(Q), node[0], f_opt)
continue
node = node[1]
# Solve the node
result = solver(node)
# Local solution data
x = result['x']
f = result['f'].get()[0]
# Store continuous solution data if none has been stored yet
if x0 is None:
x0 = casadi.DMatrix(x)
f0 = f
# Check if branch can be fathomed
if f >= f_opt:
print "Node %4d (%4d left): %9g >= %9g - POST-FATHOM" % (seqnum, len(Q), f, f_opt)
continue
# Check for violations of integrality (fixed tolerance 1e-5)
viol = [abs(casadi.floor(x[i] + 0.5) - x[i]) for i in integers]
idx = [(integers[i], viol[i]) for i in range(len(integers)) if viol[i] > 1e-5]
if not idx:
# Register new global solution
x_opt = x
f_opt = f
# Cull the branch and bound tree
pre = len(Q)
Q = [n for n in Q if n[0] < f_opt]
post = len(Q)
print "Node %4d (%4d left): f_opt = %9g - *** SOLUTION *** (%d culled)" % (seqnum, len(Q), f, pre - post)
else:
# Branch on first violation
idx = idx[0][0]
# Generate two new nodes (could reuse node structure)
ln = {
'x0': casadi.DMatrix(x),
'lbx': node['lbx'],
'ubx': casadi.DMatrix(node['ubx']),
'lbg': node['lbg'],
'ubg': node['ubg'],
'lam_x0': casadi.DMatrix(result['lam_x']),
'lam_g0': casadi.DMatrix(result['lam_g'])
}
un = {
'x0': casadi.DMatrix(x),
'lbx': casadi.DMatrix(node['lbx']),
'ubx': node['ubx'],
'lbg': node['lbg'],
'ubg': node['ubg'],
'lam_x0': casadi.DMatrix(result['lam_x']),
'lam_g0': casadi.DMatrix(result['lam_g'])
}
ln['ubx'][idx] = casadi.floor(x[idx])
un['lbx'][idx] = casadi.ceil(x[idx])
lower_node = (f, ln)
upper_node = (f, un)
# Insert new nodes in queue (inefficient for large queues)
Q.extend([lower_node, upper_node])
Q.sort(cmp=lambda x,y: cmp(y[0], x[0]))
print "Node %4d (%4d left): %9g - BRANCH ON %d" % (seqnum, len(Q), f, idx)
return {
'x0': x0,
'f0': f0,
'x': x_opt,
'f': f_opt
}
# Converts FEniCS matrix to scipy.sparse.coo_matrix
def matrix_to_coo(A, shape=None):
nnz = A.nnz()
col = numpy.empty(nnz, dtype='uint64')
row = numpy.empty(nnz, dtype='uint64')
val = numpy.empty(nnz)
if shape is None:
shape = (A.size(0), A.size(1))
it = 0
for i in range(A.size(0)):
col_local, val_local = A.getrow(i)
nnz_local = col_local.shape[0]
col[it:it+nnz_local] = col_local[:]
row[it:it+nnz_local] = i
val[it:it+nnz_local] = val_local[:]
it += nnz_local
return scipy.sparse.coo_matrix((val, (row, col)), shape=shape)
# Returns FEniCS expression for elementary source term
def source_term(x0):
return Expression("100.0 * exp(-pow(x[0] - x0, 2) / 0.02)", x0=x0)
# Grid resolutions
nx = 128
nu = 8
# Generate mesh and function space
mesh = UnitIntervalMesh(nx)
V = FunctionSpace(mesh, 'CG', 1)
# Define the bilinear form and assemble it
u = TrialFunction(V)
v = TestFunction(V)
a = inner(grad(u), grad(v)) * dx + u * v * ds
A = assemble(a)
# Create the linear form for the exact source term and perform assembly
f = source_term(3.0 / math.pi) + source_term(0.5)
L = f * v * dx
b = assemble(L)
# Solve for the reference solution
u_ref = Function(V)
solve(A, u_ref.vector(), b)
# Define the control grid and the elementary source terms
ctrl_grid = numpy.linspace(0.0, 1.0, num=nu+1)[:-1]
ctrl_grid += 0.5 * ctrl_grid[1]
src_expr = [source_term(x0) for x0 in ctrl_grid]
# Assemble the linear forms corresponding to the elementary source terms and
# construct the second half of the coefficient matrix
b = [assemble(-f * v * dx) for f in src_expr]
B = scipy.column_stack([v.array() for v in b])
# Construct the full coefficient matrix
C = scipy.sparse.vstack([
scipy.sparse.hstack([matrix_to_coo(A), B]),
scipy.sparse.coo_matrix(([1.0]*nu, ([0]*nu, [V.dim() + i for i in range(nu)])), shape=(1, V.dim() + nu))
])
# Transfer the optimization constraints to CasADi
C = casadi.DMatrix(C)
lb = casadi.DMatrix.zeros(C.shape[0], 1)
ub = casadi.DMatrix.zeros(C.shape[0], 1)
lb[-1] = 0.0
ub[-1] = 5.0
lbx = numpy.array([-numpy.inf]*V.dim() + [0.0]*nu)
ubx = numpy.array([ numpy.inf]*V.dim() + [1.0]*nu)
# Define the objective functional and assemble it
u = Function(V)
J = (u_ref - u)**2 * dx
dJdu = derivative(J, u)
dJdu2 = derivative(dJdu, u)
H = casadi.DMatrix(matrix_to_coo(assemble(dJdu2), shape=(V.dim() + nu, V.dim() + nu)))
g = casadi.DMatrix(numpy.concatenate((assemble(dJdu).array(), [0.0]*nu)))
c = assemble(J)
# Build the CasADi NLP
x = casadi.MX.sym('X', V.dim() + nu)
nlp = casadi.MXFunction('nlp',
casadi.nlpIn(x=x),
casadi.nlpOut(
f=0.5*casadi.quad_form(x, H) + casadi.inner_prod(g, x) + c,
g=casadi.mul(C, x)
))
# Build NLP solver
solver = casadi.NlpSolver('solver', 'ipopt', nlp, {
'print_level': 0,
'print_time': False
})
result = solve_bnb(solver, {
'lbx': lbx,
'ubx': ubx,
'lbg': lb,
'ubg': ub
}, range(V.dim(), V.dim() + nu))
# Evaluate result
print ""
print "----------------------------"
print " f = %g" % result['f']
u.vector()[:] = result['x'][:V.dim()].toArray()[:,0]
Results
Node solutions are calculated using IPOPT (3.12, default settings, using linear solver MUMPS on Ubuntu 15.10 for x86-64 with Linux 4.2.0-19-generic, Intel(R) Core(TM) i7-4790K CPU @ 4.00GHz, 16 GB RAM). The objective function value is 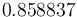. The integer solution is found after processing 25 nodes.