Source Inversion (FEniCS/Casadi)
This page contains a discretized version of the mixed integer PDE constrained optimization problem Source Inversion in CasADi 2.4.3 format. The weak version of the problem was discretized using finite element methods (via FEniCS) using first-degree Lagrangian elements on an equidistant mesh with 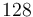 cells.
cells.
CasADi
from dolfin import * import math import numpy import scipy, scipy.sparse import casadi # Simple Branch and Bound solver def solve_bnb(solver, root, integers): # Initialize the node queue Q = [(numpy.inf, root)] # Global solution data x_opt = None f_opt = numpy.inf # Continuous solution data x0 = None f0 = numpy.inf # Main loop seqnum = 0 while Q: seqnum += 1 # Extract node with lowest lower bound and check if fathoming is necessary # (should not happen) node = Q.pop() if f_opt < numpy.inf and node[0] >= f_opt: print "Node %4d (%4d left): %9g >= %9g - PRE-FATHOM" % (seqnum, len(Q), node[0], f_opt) continue node = node[1] # Solve the node result = solver(node) # Local solution data x = result['x'] f = result['f'].get()[0] # Store continuous solution data if none has been stored yet if x0 is None: x0 = casadi.DMatrix(x) f0 = f # Check if branch can be fathomed if f >= f_opt: print "Node %4d (%4d left): %9g >= %9g - POST-FATHOM" % (seqnum, len(Q), f, f_opt) continue # Check for violations of integrality (fixed tolerance 1e-5) viol = [abs(casadi.floor(x[i] + 0.5) - x[i]) for i in integers] idx = [(integers[i], viol[i]) for i in range(len(integers)) if viol[i] > 1e-5] if not idx: # Register new global solution x_opt = x f_opt = f # Cull the branch and bound tree pre = len(Q) Q = [n for n in Q if n[0] < f_opt] post = len(Q) print "Node %4d (%4d left): f_opt = %9g - *** SOLUTION *** (%d culled)" % (seqnum, len(Q), f, pre - post) else: # Branch on first violation idx = idx[0][0] # Generate two new nodes (could reuse node structure) ln = { 'x0': casadi.DMatrix(x), 'lbx': node['lbx'], 'ubx': casadi.DMatrix(node['ubx']), 'lbg': node['lbg'], 'ubg': node['ubg'], 'lam_x0': casadi.DMatrix(result['lam_x']), 'lam_g0': casadi.DMatrix(result['lam_g']) } un = { 'x0': casadi.DMatrix(x), 'lbx': casadi.DMatrix(node['lbx']), 'ubx': node['ubx'], 'lbg': node['lbg'], 'ubg': node['ubg'], 'lam_x0': casadi.DMatrix(result['lam_x']), 'lam_g0': casadi.DMatrix(result['lam_g']) } ln['ubx'][idx] = casadi.floor(x[idx]) un['lbx'][idx] = casadi.ceil(x[idx]) lower_node = (f, ln) upper_node = (f, un) # Insert new nodes in queue (inefficient for large queues) Q.extend([lower_node, upper_node]) Q.sort(cmp=lambda x,y: cmp(y[0], x[0])) print "Node %4d (%4d left): %9g - BRANCH ON %d" % (seqnum, len(Q), f, idx) return { 'x0': x0, 'f0': f0, 'x': x_opt, 'f': f_opt } # Converts FEniCS matrix to scipy.sparse.coo_matrix def matrix_to_coo(A, shape=None): nnz = A.nnz() col = numpy.empty(nnz, dtype='uint64') row = numpy.empty(nnz, dtype='uint64') val = numpy.empty(nnz) if shape is None: shape = (A.size(0), A.size(1)) it = 0 for i in range(A.size(0)): col_local, val_local = A.getrow(i) nnz_local = col_local.shape[0] col[it:it+nnz_local] = col_local[:] row[it:it+nnz_local] = i val[it:it+nnz_local] = val_local[:] it += nnz_local return scipy.sparse.coo_matrix((val, (row, col)), shape=shape) # Returns FEniCS expression for elementary source term def source_term(x0): return Expression("100.0 * exp(-pow(x[0] - x0, 2) / 0.02)", x0=x0) # Grid resolutions nx = 128 nu = 8 # Generate mesh and function space mesh = UnitIntervalMesh(nx) V = FunctionSpace(mesh, 'CG', 1) # Define the bilinear form and assemble it u = TrialFunction(V) v = TestFunction(V) a = inner(grad(u), grad(v)) * dx + u * v * ds A = assemble(a) # Create the linear form for the exact source term and perform assembly f = source_term(3.0 / math.pi) + source_term(0.5) L = f * v * dx b = assemble(L) # Solve for the reference solution u_ref = Function(V) solve(A, u_ref.vector(), b) # Define the control grid and the elementary source terms ctrl_grid = numpy.linspace(0.0, 1.0, num=nu+1)[:-1] ctrl_grid += 0.5 * ctrl_grid[1] src_expr = [source_term(x0) for x0 in ctrl_grid] # Assemble the linear forms corresponding to the elementary source terms and # construct the second half of the coefficient matrix b = [assemble(-f * v * dx) for f in src_expr] B = scipy.column_stack([v.array() for v in b]) # Construct the full coefficient matrix C = scipy.sparse.vstack([ scipy.sparse.hstack([matrix_to_coo(A), B]), scipy.sparse.coo_matrix(([1.0]*nu, ([0]*nu, [V.dim() + i for i in range(nu)])), shape=(1, V.dim() + nu)) ]) # Transfer the optimization constraints to CasADi C = casadi.DMatrix(C) lb = casadi.DMatrix.zeros(C.shape[0], 1) ub = casadi.DMatrix.zeros(C.shape[0], 1) lb[-1] = 0.0 ub[-1] = 5.0 lbx = numpy.array([-numpy.inf]*V.dim() + [0.0]*nu) ubx = numpy.array([ numpy.inf]*V.dim() + [1.0]*nu) # Define the objective functional and assemble it u = Function(V) J = (u_ref - u)**2 * dx dJdu = derivative(J, u) dJdu2 = derivative(dJdu, u) H = casadi.DMatrix(matrix_to_coo(assemble(dJdu2), shape=(V.dim() + nu, V.dim() + nu))) g = casadi.DMatrix(numpy.concatenate((assemble(dJdu).array(), [0.0]*nu))) c = assemble(J) # Build the CasADi NLP x = casadi.MX.sym('X', V.dim() + nu) nlp = casadi.MXFunction('nlp', casadi.nlpIn(x=x), casadi.nlpOut( f=0.5*casadi.quad_form(x, H) + casadi.inner_prod(g, x) + c, g=casadi.mul(C, x) )) # Build NLP solver solver = casadi.NlpSolver('solver', 'ipopt', nlp, { 'print_level': 0, 'print_time': False }) result = solve_bnb(solver, { 'lbx': lbx, 'ubx': ubx, 'lbg': lb, 'ubg': ub }, range(V.dim(), V.dim() + nu)) # Evaluate result print "" print "----------------------------" print " f = %g" % result['f'] u.vector()[:] = result['x'][:V.dim()].toArray()[:,0]
Results
Node solutions are calculated using IPOPT (3.12, default settings, using linear solver MUMPS on Ubuntu 15.10 for x86-64 with Linux 4.2.0-19-generic, Intel(R) Core(TM) i7-4790K CPU @ 4.00GHz, 16 GB RAM). The objective function value is 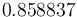 . The integer solution is found after processing 25 nodes.
. The integer solution is found after processing 25 nodes.
Solution
The following is a Gnuplot compatible tabular version of the control data determined by the solver:
# x w w0 0.0625 0 2.91549e-08 0.1875 0 2.75108e-08 0.3125 0 6.746e-08 0.4375 1 0.46917 0.5625 0 0.543817 0.6875 0 1.33205e-07 0.8125 0 1.51069e-07 0.9375 1 0.897707
The following is a Gnuplot compatible tabular version of the solution found using FEM approximations:
# x u u0
0 19.845 18.7521
0.0078125 20.0001 18.8986
0.015625 20.1551 19.0451
0.0234375 20.3101 19.1916
0.03125 20.4652 19.3381
0.0390625 20.6202 19.4846
0.046875 20.7752 19.6311
0.0546875 20.9303 19.7776
0.0625 21.0853 19.9241
0.0703125 21.2403 20.0706
0.078125 21.3953 20.2171
0.0859375 21.5503 20.3635
0.09375 21.7053 20.51
0.101562 21.8603 20.6565
0.109375 22.0153 20.8029
0.117188 22.1702 20.9494
0.125 22.3251 21.0958
0.132812 22.4799 21.2422
0.140625 22.6347 21.3886
0.148438 22.7894 21.5349
0.15625 22.944 21.6812
0.164062 23.0985 21.8275
0.171875 23.2528 21.9737
0.179688 23.407 22.1197
0.1875 23.561 22.2657
0.195312 23.7146 22.4116
0.203125 23.868 22.5573
0.210938 24.0209 22.7028
0.21875 24.1734 22.848
0.226562 24.3254 22.993
0.234375 24.4766 23.1377
0.242188 24.6271 23.282
0.25 24.7767 23.4259
0.257812 24.9252 23.5692
0.265625 25.0725 23.7119
0.273438 25.2184 23.854
0.28125 25.3627 23.9952
0.289062 25.5052 24.1355
0.296875 25.6457 24.2748
0.304688 25.7839 24.413
0.3125 25.9196 24.5498
0.320312 26.0525 24.6852
0.328125 26.1823 24.8189
0.335938 26.3088 24.9509
0.34375 26.4316 25.0809
0.351562 26.5505 25.2087
0.359375 26.6651 25.3342
0.367188 26.7753 25.4572
0.375 26.8807 25.5774
0.382812 26.9811 25.6947
0.390625 27.0762 25.8089
0.398438 27.1659 25.9198
0.40625 27.2499 26.0271
0.414062 27.3281 26.1308
0.421875 27.4004 26.2305
0.429688 27.4666 26.3262
0.4375 27.5268 26.4177
0.445312 27.5809 26.5047
0.453125 27.6289 26.5873
0.460938 27.6708 26.6652
0.46875 27.7069 26.7384
0.476562 27.7371 26.8066
0.484375 27.7617 26.87
0.492188 27.7808 26.9283
0.5 27.7947 26.9816
0.507812 27.8035 27.0298
0.515625 27.8076 27.0729
0.523438 27.8072 27.1109
0.53125 27.8026 27.1438
0.539062 27.794 27.1718
0.546875 27.7818 27.1948
0.554688 27.7662 27.213
0.5625 27.7476 27.2264
0.570312 27.7261 27.2352
0.578125 27.7021 27.2395
0.585938 27.6759 27.2394
0.59375 27.6476 27.2351
0.601562 27.6174 27.2269
0.609375 27.5857 27.2147
0.617188 27.5525 27.199
0.625 27.5181 27.1797
0.632812 27.4826 27.1573
0.640625 27.4461 27.1317
0.648438 27.4087 27.1032
0.65625 27.3706 27.0721
0.664062 27.3318 27.0385
0.671875 27.2924 27.0025
0.679688 27.2525 26.9644
0.6875 27.2119 26.9242
0.695312 27.1709 26.8821
0.703125 27.1293 26.8383
0.710938 27.0871 26.7928
0.71875 27.0443 26.7457
0.726562 27.0008 26.6971
0.734375 26.9566 26.6469
0.742188 26.9115 26.5953
0.75 26.8654 26.5422
0.757812 26.8183 26.4875
0.765625 26.7699 26.4312
0.773438 26.72 26.3732
0.78125 26.6686 26.3135
0.789062 26.6153 26.2517
0.796875 26.56 26.188
0.804688 26.5024 26.1219
0.8125 26.4423 26.0534
0.820312 26.3794 25.9822
0.828125 26.3134 25.9082
0.835938 26.244 25.8311
0.84375 26.171 25.7506
0.851562 26.094 25.6665
0.859375 26.0129 25.5785
0.867188 25.9272 25.4865
0.875 25.8368 25.3902
0.882812 25.7413 25.2893
0.890625 25.6406 25.1837
0.898438 25.5345 25.0732
0.90625 25.4227 24.9576
0.914062 25.305 24.8368
0.921875 25.1815 24.7107
0.929688 25.0519 24.5791
0.9375 24.9162 24.4421
0.945312 24.7745 24.2996
0.953125 24.6267 24.1516
0.960938 24.4728 23.9982
0.96875 24.313 23.8395
0.976562 24.1474 23.6756
0.984375 23.9762 23.5067
0.992188 23.7995 23.3328
1 23.6175 23.1542