Robot arm problem

Robot arm problem
State dimension:	1
Differential states:	3
Continuous control functions:	3
Path constraints:	12
Interior point equalities:	12

The robot arm problem focuses on minimizing the time used by a robot arm to move from an origin to a destination. The arm is a bar of length 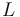$L$ and sticks out distance 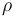$\rho$ from its moving axis, while sticking out distance 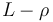$L - \rho$ in the other direction. The problem can be found in [Moessner1995]Address: Im Neuenheimer Feld 368, 69120 Heidelberg, Germany
Author: M. Moessner-Beigel
Month: November
School: Ruprecht-Karls-Universit\"at Heidelberg
Title: Optimale Steuerung f\"ur Industrieroboter unter Ber\"ucksichtigung der getriebebedingten Elastizit\"at
Type: Diplomarbeit
Year: 1995
or in the COPS library.

Model formulation

The problem is set up using the length 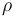$\rho$, "the vertical angles 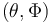$(\theta, \Phi)$ from the horizontal plane, the controls 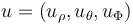$u=(u_{\rho},u_{\theta},u_{\Phi})$ and the final time $t_f$".

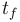The moving robot is modelled with the following equations:

$\ddot{\rho} = \frac{u_{\rho}}{L}, \qquad \ddot{\theta} = \frac{u_{\theta}}{I_{\theta}}, \qquad \ddot{\Phi} = \frac{u_{\Phi}}{I_{\Phi}}$

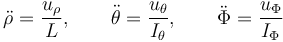
where 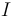$I$ characterizes the moment of inertia, i.e.

$\begin{array}{ccl} I_{\theta} & = & \frac{((L-\rho)^3 + \rho^3)}{3} \cdot \sin(\Phi)^2, \\ I_{\Phi} & = & \frac{((L-\rho)^3 + \rho^3)}{3}. \end{array}$

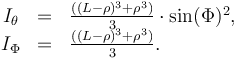
The path constraints on the states 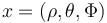$x= (\rho, \theta, \Phi)$ and on the controls 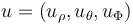$u = (u_{\rho},u_{\theta},u_{\Phi})$ as well as the boundary conditions can be seen in the optimization problem further down.

Optimization problem

$\begin{array}{llclr} \displaystyle \min_{x, u, t_f} & t_f \\[1.5ex] \mbox{s.t.} & \ddot{\rho} & = & \frac{u_{\rho}}{L}, \\ & \ddot{\theta} & = & \frac{u_{\theta}}{I_{\theta}}, \\ & \ddot{\Phi} & = & \frac{u_{\Phi}}{I_{\Phi}}, \\[1.5ex] & x(0) &=& (4.5, 0, \frac{\pi}{4})^T, \\ & x(t_f) &=& (4.5, \frac{2\pi}{3}, \frac{\pi}{4})^T, \\ & \dot{x}(0) &=& (0,0,0)^T, \\ & \dot{x}(t_f) &=& (0,0,0)^T, \\[1.5ex] & \rho(t) & \in & [0,L],\\ & \theta(t) & \in & [-\pi, \pi],\\ & \Phi(t) & \in & [0, \pi],\\ & u_{\rho} & \leq & 1,\\ & u_{\theta} & \leq & 1,\\ & u_{\Phi} & \leq & 1.\\ \end{array}$

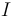where $I$ is the moment of inertia as above.

Source Code

Model descriptions are available in

• AMPL/TACO code at Robot arm problem (TACO)

== References ==

[Moessner1995]

M. Moessner-Beigel: Optimale Steuerung f\"ur Industrieroboter unter Ber\"ucksichtigung der getriebebedingten Elastizit\"at, 1995