Category:Gekko
The GEKKO Python package solves large-scale mixed-integer and differential algebraic equations with nonlinear programming solvers (IPOPT, APOPT, BPOPT, SNOPT, MINOS). Modes of operation include machine learning, data reconciliation, real-time optimization, dynamic simulation, and nonlinear model predictive control. In addition, the package solves Linear programming (LP), Quadratic programming (QP), Quadratically constrained quadratic program (QCQP), Nonlinear programming (NLP), Mixed integer programming (MIP), and Mixed integer linear programming (MILP). GEKKO is available in Python and installed with pip from PyPI of the Python Software Foundation.
pip install gekko
GEKKO works on all platforms (Windows, MacOS, Linux, ARM processors) and with Python 2.7 and 3+. By default, the problem is sent to a public server where the solution is computed and returned to Python. There is a Windows and Linux option to solve without an Internet connection. GEKKO is an extension of the APMonitor Optimization Suite but has integrated the modeling and solution visualization directly within Python. A mathematical model is expressed in terms of variables and equations such as the Hock & Schittkowski Benchmark Problem #71 used to test the performance of nonlinear programming solvers. This particular optimization problem has an objective function 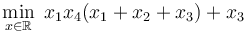 and subject to the inequality constraint
and subject to the inequality constraint 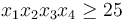 and equality constraint
and equality constraint 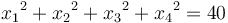 . The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are
. The four variables must be between a lower bound of 1 and an upper bound of 5. The initial guess values are 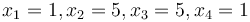 . This optimization problem is solved with GEKKO as shown below.
. This optimization problem is solved with GEKKO as shown below.
from gekko import GEKKO m = GEKKO() # Initialize gekko # Initialize variables x1 = m.Var(value=1,lb=1,ub=5) x2 = m.Var(value=5,lb=1,ub=5) x3 = m.Var(value=5,lb=1,ub=5) x4 = m.Var(value=1,lb=1,ub=5) # Equations m.Equation(x1*x2*x3*x4>=25) m.Equation(x1**2+x2**2+x3**2+x4**2==40) m.Obj(x1*x4*(x1+x2+x3)+x3) # Objective m.solve(disp=False) # Solve print('x1: ' + str(x1.value)) print('x2: ' + str(x2.value)) print('x3: ' + str(x3.value)) print('x4: ' + str(x4.value)) print('Objective: ' + str(m.options.objfcnval))
External links
- GEKKO on Wikipedia
- GEKKO Documentation
- GEKKO Source Code
- GEKKO on PyPI for Python pip install
- GEKKO is open-source product of National Science Foundation (NSF) research grant 1547110
- References to APMonitor and GEKKO in the literature
- 18 examples of GEKKO: machine learning, optimal control, data regression
Pages in category "Gekko"
The following 6 pages are in this category, out of 6 total.