Category:Elliptic
From mintOC
This category contains all control problems which are governed by an elliptic partial differential equation.
A second order linear partial differential equation can be written as
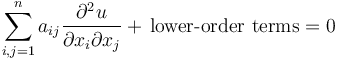 .
.
If the matrix 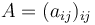 is positive or negative definite, the partial differential equation is called elliptic.
is positive or negative definite, the partial differential equation is called elliptic.
An example is the Poisson's equation: 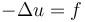 ,
where
,
where  denotes the Laplace operator,
denotes the Laplace operator, 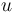 is the unknown, and the function
is the unknown, and the function 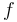 is given.
is given.
Pages in category "Elliptic"
The following 2 pages are in this category, out of 2 total.