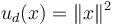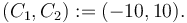Controlled Heating
The controlled heating problem is a simple problem from the domain of continuous PDE constrained optimal control. The goal is to parametrize the heat equation under Robin-type boundary conditions such that the stationary solution tracks a predefined reference function. This is equivalent to solving Poisson's problem under Robin-type boundary equations. The problem is therefore closely related to the source inversion problem. As opposed to the source inversion problem however, the controlled heating problem does not require the source term to be a linear combination of elementary source terms. The source term can be an arbitrary function which is usually chosen from the same function space as the temperature function.
Contents
[hide]Problem Statement
Let 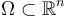 be a contiguous domain and let
be a contiguous domain and let 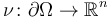 be an outer unit normal of
be an outer unit normal of 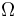 . The Poisson problem with simple Robin-type boundary conditions then takes the following form:
. The Poisson problem with simple Robin-type boundary conditions then takes the following form:
Here, 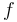 denotes the source term. We demand that
denotes the source term. We demand that 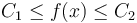 in
in 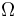 . Given a reference function
. Given a reference function 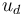 , the optimization problem is given by:
, the optimization problem is given by:
Weak formulation
Some PDE discretization techniques (such as finite element methods) require the use of weak formulations of the original problem. The weak formulation of the Poisson problem with Robin-type boundary conditions as described above is obtained using Green's identities:
Here, 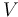 is a suitable space of test functions. The optimization problem then takes the following form:
is a suitable space of test functions. The optimization problem then takes the following form:
Parameters
For testing purposes, we consider 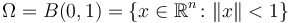 with
with 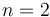 . The reference function is given by:
. The reference function is given by:
Additionally, let
Reference solution
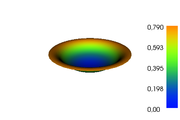
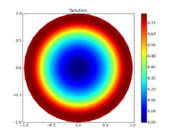
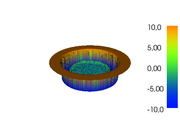
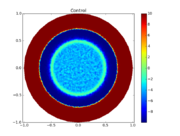
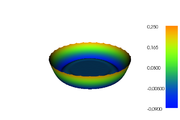
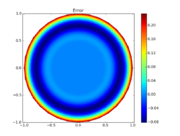
The reference solution was generated using finite element discretizations. The mesh was generated using FEniCS' mesh generation component with a resolution setting of 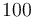 . The function space was constructed using first-degree Lagrangian elements. The optimization problem was solved using CasADi's IPOPT interface. The exact code used to solve the problem alongside solution data can be found under Controlled Heating (FEniCS/Casadi). The optimal objective function value is
. The function space was constructed using first-degree Lagrangian elements. The optimization problem was solved using CasADi's IPOPT interface. The exact code used to solve the problem alongside solution data can be found under Controlled Heating (FEniCS/Casadi). The optimal objective function value is 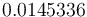 .
.
- Reference solution plots
Source Code
Model descriptions are available in
- Casadi code using FEniCS at Controlled Heating (FEniCS/Casadi)
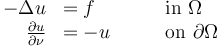
![\begin{array}[t]{rl}
\min\limits_{u,f} & \int\limits_\Omega (u - u_d)^2 \, \mathrm{d}x \\
\text{s.t.} & \begin{array}[t]{rll}
- \Delta u(x) &= f(x) \qquad & \forall x \in \Omega \\[1.5ex]
\frac{\partial u}{\partial \nu}(x) &= -u(x) \qquad & \forall x \in \partial \Omega \\
f(x) &\in [C_1, C_2] \qquad & \forall x \in \Omega
\end{array}
\end{array}](https://mintoc.de/images/math/7/2/0/720e99ba6037b8996e46f01cbfb2d2e8.png)
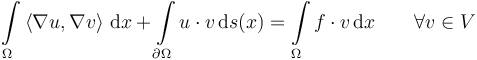
![\begin{array}[t]{rl}
\min\limits_{u,f} & \int\limits_\Omega (u - u_d)^2 \, \mathrm{d}x \\
\text{s.t.} & \begin{array}[t]{rll}
\int\limits_\Omega \left\langle \nabla u, \nabla v \right\rangle \,\mathrm{d}x + \int\limits_{\partial \Omega} u \cdot v \,\mathrm{d}s(x) &= \int\limits_\Omega f \cdot v \,\mathrm{d}x \qquad &\forall v \in V \\[1.5ex]
f(x) &\in [C_1, C_2] \qquad & \forall x \in \Omega
\end{array}
\end{array}](https://mintoc.de/images/math/6/6/5/66506479a74c34a4bb3269b8733bd743.png)