Controlled Heating (FEniCS/Casadi)

This page contains a discretized version of the PDE constrained optimization problem Controlled Heating in CasADi 2.4.3 format. The weak version of the problem was discretized using finite element methods (via FEniCS) using first-degree Lagrangian elements on a mesh automatically generated using FEniCS' mesh generation component.

CasADi

from dolfin import *
import mshr
 
import numpy
import scipy, scipy.sparse
import casadi
 
 
# Converts FEniCS matrix to scipy.sparse.coo_matrix
def matrix_to_coo(A, shape=None):
    nnz = A.nnz()
    col = numpy.empty(nnz, dtype='uint64')
    row = numpy.empty(nnz, dtype='uint64')
    val = numpy.empty(nnz)
 
    if shape is None:
        shape = (A.size(0), A.size(1))
 
    it = 0
    for i in range(A.size(0)):
        col_local, val_local = A.getrow(i)
        nnz_local = col_local.shape[0]
 
        col[it:it+nnz_local] = col_local[:]
        row[it:it+nnz_local] = i
        val[it:it+nnz_local] = val_local[:]
        it                  += nnz_local
 
    return scipy.sparse.coo_matrix((val, (row, col)), shape=shape)
 
# Construct a high-resolution mesh of the unit circle
domain   = mshr.Circle(Point(0.0, 0.0), 1.0)
mesh     = mshr.generate_mesh(domain, 100)
 
# Define the function space
V = FunctionSpace(mesh, 'CG', 1)
 
# Define trial and test functions
h = TrialFunction(V)
t = TrialFunction(V)
v = TestFunction(V)
 
# Construct the two parts of the constraint matrix and assemble them
lhs_t = inner(grad(t), grad(v)) * dx + t * v * ds
lhs_h = -h * v * dx
 
A = matrix_to_coo(assemble(lhs_t))
B = matrix_to_coo(assemble(lhs_h))
C = casadi.DMatrix(scipy.sparse.hstack([A, B]))
 
# Data structures for solution data
sol     = Function(V)
control = Function(V)
 
# Define objective functional and assemble it
sol_ref = interpolate(Expression("x[0] * x[0] + x[1] * x[1]"), V)
J       = pow(sol_ref - sol, 2) * dx
J_grad  = derivative(J, sol)
J_hess  = derivative(J_grad, sol)
 
c = assemble(J)
g = casadi.DMatrix(numpy.concatenate((assemble(J_grad).array(), numpy.zeros(V.dim()))))
H = casadi.DMatrix(matrix_to_coo(assemble(J_hess), shape=(2*V.dim(), 2*V.dim())))
 
# Construct CasADi problem
X = casadi.MX.sym('X', V.dim() * 2)
nlp = casadi.MXFunction('nlp', casadi.nlpIn(x=X), casadi.nlpOut(
    f=0.5*casadi.quad_form(X, H) + casadi.inner_prod(g, X) + c,
    g=casadi.mul(C, X)
))
 
# Construct CasADi solver and solve problem
solver = casadi.NlpSolver('solver', 'ipopt', nlp)
result = solver({
    'lbx': [-numpy.inf] * V.dim() + [-10.0] * V.dim(),
    'ubx': [ numpy.inf] * V.dim() + [ 10.0] * V.dim(),
    'lbg': 0.0,
    'ubg': 0.0
})
 
# Evaluate results
sol.vector()[:] = result['x'][:V.dim()].toArray()[:,0]
control.vector()[:] = result['x'][V.dim():].toArray()[:,0]
 
error = Function(V)
error.assign(sol_ref - sol)

Results

The solutions is calculated using IPOPT (3.12, default settings, using linear solver MUMPS on Ubuntu 15.10 for x86-64 with Linux 4.2.0-19-generic, Intel(R) Core(TM) i7-4790K CPU @ 4.00GHz, 16 GB RAM). The solution process The objective function value is 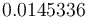$0.0145336$. IPOPT finds the solution in 17 iterations (62.060 seconds proc time).

Solution

A Gnuplot compatible tabular version of the solution data is provided separately.