Difference between revisions of "Category:Elliptic"
From mintOC
FelixMueller (Talk | contribs) |
FelixMueller (Talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
This category contains all control problems which are governed by an elliptic partial differential equation. | This category contains all control problems which are governed by an elliptic partial differential equation. | ||
| − | [[Category: Model characterization]] [[Category: PDE model]] | + | <p> |
| + | A second order linear partial differential equation can be written as | ||
| + | <math>\sum^n_{i,j=1} a_{ij} \frac{\partial^2u}{\partial x_i \partial x_j} +\, \text{lower-order terms} = 0</math>. | ||
| + | </p> | ||
| + | |||
| + | <p> | ||
| + | If the matrix <math>A=(a_{ij})_{ij}</math> is positive or negative definite, the partial differential equation is called elliptic. | ||
| + | </p> | ||
| + | <p> | ||
| + | An example is the Poisson's equation: <math>-\Delta u = f</math>, | ||
| + | where <math>\Delta</math> denotes the Laplace operator, <math>u</math> is the unknown, and the function <math>f</math> is given. | ||
| + | </p> | ||
| + | |||
| + | |||
| + | <!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> | ||
| + | |||
| + | [[Category: Model characterization]] | ||
| + | [[Category: PDE model]] | ||
Latest revision as of 16:22, 24 February 2016
This category contains all control problems which are governed by an elliptic partial differential equation.
A second order linear partial differential equation can be written as
.
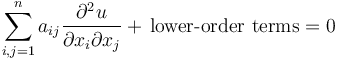If the matrix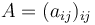 
is positive or negative definite, the partial differential equation is called elliptic.
An example is the Poisson's equation: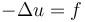 
,
where 
denotes the Laplace operator,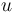 
is the unknown, and the function 
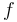is given.
Pages in category "Elliptic"
The following 2 pages are in this category, out of 2 total.
