Difference between revisions of "Category:Path-constrained arcs"
JonasSchulze (Talk | contribs) m (Text replacement - "\<bibref\>(.*)\<\/bibref\>" to "<bib id="$1" />") |
JonasSchulze (Talk | contribs) m (Text replacement - "<bibreferences/>" to "<biblist />") |
||
| Line 2: | Line 2: | ||
== References == | == References == | ||
| − | < | + | <biblist /> |
[[Category:Solution characterization]] | [[Category:Solution characterization]] | ||
Latest revision as of 11:10, 23 January 2016
Whenever a path constraint is active, i.e., it holds ![c_i(x(t)) = 0 \; \forall \; t \in [t^\text{start}, t^\text{end}] \subseteq [0, t_f]](https://mintoc.de/images/math/b/2/a/b2ae1f8d2da30f32c01f209278698096.png)
, and no continuous control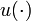 
can be determined to compensate for the changes in 
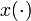, naturally 
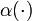needs to do so by taking values in the interior of its feasible domain. An illustrating example has been given in [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
Journal: Mathematical Programming
Number: 1
Pages: 109--149
Title: Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems
Url: http://mathopt.de/PUBLICATIONS/Sager2009.pdf
Volume: 118
Year: 2009
, where velocity limitations for the energy-optimal operation of New York subway trains are taken into account. The optimal integer solution does only exist in the limit case of infinite switching (Zeno behavior), or when a tolerance is given.
References
| [Sager2009] | Sager, S.; Reinelt, G.; Bock, H.G. (2009): Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems. Mathematical Programming, 118, 109--149 | |
Pages in category "Path-constrained arcs"
The following 10 pages are in this category, out of 10 total.
