Difference between revisions of "Direct Current Transmission Heating Problem"
(Created page with "{{Dimensions |nd = 1 |nx = 3 |nw = 1 |nre = 3 }} The '''direct current transfer heating problem''' models a simplified flow of direct electrical cu...") |
|||
| Line 8: | Line 8: | ||
The '''direct current transfer heating problem''' models a simplified flow of direct electrical current within an electrical network with defined producers and consumers of electrical power. The model includes heating and cooling that occurs in electrical conductors due to specific resistance and heat exchange with the surrounding air. An optimal strategy for regulating the power production of individual producers as well as voltages and currents on specific conductors with the goal of minimizing the net power loss due to heating on all power lines over a fixed time horizon while fully supplying all consumers. | The '''direct current transfer heating problem''' models a simplified flow of direct electrical current within an electrical network with defined producers and consumers of electrical power. The model includes heating and cooling that occurs in electrical conductors due to specific resistance and heat exchange with the surrounding air. An optimal strategy for regulating the power production of individual producers as well as voltages and currents on specific conductors with the goal of minimizing the net power loss due to heating on all power lines over a fixed time horizon while fully supplying all consumers. | ||
| − | The model is largely assembled from well-known basic descriptions of phenomena easily accessible to the audience of high-school level physics courses. Mainly, these are [https://en.wikipedia.org/wiki/Ohm's_law Ohm's law], [https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity electrical resistivity], [https://en.wikipedia.org/wiki/Joule_heating Joule heating] and [https://en.wikipedia.org/wiki/Thermal_conductivity thermal conductivity]. Note that changes of resistivity with temperature are taken into account. | + | The model is largely assembled from well-known basic descriptions of phenomena easily accessible to the audience of high-school level physics courses. Mainly, these are [https://en.wikipedia.org/wiki/Ohm's_law Ohm's law], [https://en.wikipedia.org/wiki/Electrical_resistivity_and_conductivity electrical resistivity], [https://en.wikipedia.org/wiki/Joule_heating Joule heating] and [https://en.wikipedia.org/wiki/Thermal_conductivity thermal conductivity]. Note that changes of resistivity with respect to conductor temperature are taken into account. |
== Physical background == | == Physical background == | ||
| − | The aim of the controller in this model is to provide all consumers with their required amount of [https://en.wikipedia.org/wiki/Electric_power electric power]. Electric power is given by the product of voltage and current <math>P = I \cdot U</math>. The electric power is brought to the consumers from producers via a network of power lines. Producers are assumed to have the capability of accurately regulating their power output within a certain range. Power lines are assumed to be solid blocks of an electrically conductive material surrounded by a layer of | + | The aim of the controller in this model is to provide all consumers with their required amount of [https://en.wikipedia.org/wiki/Electric_power electric power]. Electric power is given by the product of voltage and current <math>P = I \cdot U</math>. The electric power is brought to the consumers from producers via a network of power lines. Producers are assumed to have the capability of accurately regulating their power output within a certain range. Power lines are assumed to be solid blocks of an electrically conductive material surrounded by a layer of insulating material. Their cross-section is assumed to be constant along the entire length of the power line. Since both heating and power loss increase with current but not with voltage, it is always preferable to transfer direct current at the highest possible voltage which is allowed by the design of the power line. Therefore, only the electrical current is considered as a control. |
| + | |||
| + | The power loss in a power line is given by <math>W = I^2 \cdot R</math> where <math>R</math> is the resistance of the power line which is derived from the resistivity of the conductor using the formula | ||
| + | <p> | ||
| + | <math> | ||
| + | R = \rho \cdot \frac{l}{A} | ||
| + | </math> | ||
| + | </p> | ||
| + | where <math>\rho</math> is the resistivity of the conductor, <math>l</math> is the length of the conductor and <math>A</math> is the the cross-sectional area of the conducting material within the power line. Resistivity is assumed to vary exponentially with the temperature of the conducting material, meaning that <math>\rho = \rho_0 \cdot e^{\alpha T}</math> where <math>\rho_0</math> is the resistivity of the conducting material at room temperature (which is defined as <math>T = 0</math>) and <math>\alpha</math> is a material-specific dimensionless constant. This causes a steady power loss of | ||
| + | <p> | ||
| + | <math> | ||
| + | P_1 = \rho_0 \cdot e^{\alpha T} \cdot \frac{l}{A} \cdot I^2. | ||
| + | </math> | ||
| + | </p> | ||
| + | The lost energy is transformed into heat which raises the temperature of the conductor. As the conductor is now hotter than the air surrounding its layer of insulating material, heat is steadily lost at a rate determined by the temperature difference, the conductors surface area and the insulating material's heat conductivity. The heat loss is given by | ||
| + | <p> | ||
| + | <math> | ||
| + | P_2 = q \cdot S \cdot \Delta T | ||
| + | </math> | ||
| + | </p> | ||
| + | where <math>q</math> is the ratio between the isolating material's thermal conductivity and its thickness, <math>S</math> is the surface area of the power line and <math>\Delta T</math> is the difference between the conductor's temperature and the surrounding air's temperature (which we will assume to be the same as room temperature, i.e. <math>T = 0</math>). In summary, the rate at which the heat stored in a power line changes is given by | ||
| + | <p> | ||
| + | <math> | ||
| + | \dot{W} = P_1 - P_2 = \rho_0 \cdot e^{\alpha T} \cdot \frac{l}{A} \cdot I^2 - q \cdot l \cdot C \cdot T | ||
| + | </math> | ||
| + | </p> | ||
| + | where <math>C</math> is the circumference of the cross-section of the power line. Assuming constant density, we can use the conducting materials volume-specific heat capacity which we will refer to as <math>c</math>, we can calculate the change in temperature from the change in heat: | ||
| + | <p> | ||
| + | <math> | ||
| + | \dot{T} = \frac{\dot{W}}{c \cdot A \cdot l} = \frac{\rho_0}{c \cdot A^2} \cdot e^{\alpha T} \cdot I^2 - \frac{q \cdot C}{c \cdot A} \cdot T =: \beta_1 \cdot e^{\alpha T} \cdot I^2 - \beta_2 \cdot T. | ||
| + | </math> | ||
| + | </p> | ||
| + | |||
| + | For the examples in this article, we will assume the conductor to be solid copper surrounded by a | ||
== Mathematical formulation == | == Mathematical formulation == | ||
Revision as of 21:16, 7 December 2015
| Direct Current Transmission Heating Problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Discrete control functions: | 1 |
| Interior point equalities: | 3 |
The direct current transfer heating problem models a simplified flow of direct electrical current within an electrical network with defined producers and consumers of electrical power. The model includes heating and cooling that occurs in electrical conductors due to specific resistance and heat exchange with the surrounding air. An optimal strategy for regulating the power production of individual producers as well as voltages and currents on specific conductors with the goal of minimizing the net power loss due to heating on all power lines over a fixed time horizon while fully supplying all consumers.
The model is largely assembled from well-known basic descriptions of phenomena easily accessible to the audience of high-school level physics courses. Mainly, these are Ohm's law, electrical resistivity, Joule heating and thermal conductivity. Note that changes of resistivity with respect to conductor temperature are taken into account.
Contents
Physical background
The aim of the controller in this model is to provide all consumers with their required amount of electric power. Electric power is given by the product of voltage and current 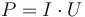 . The electric power is brought to the consumers from producers via a network of power lines. Producers are assumed to have the capability of accurately regulating their power output within a certain range. Power lines are assumed to be solid blocks of an electrically conductive material surrounded by a layer of insulating material. Their cross-section is assumed to be constant along the entire length of the power line. Since both heating and power loss increase with current but not with voltage, it is always preferable to transfer direct current at the highest possible voltage which is allowed by the design of the power line. Therefore, only the electrical current is considered as a control.
. The electric power is brought to the consumers from producers via a network of power lines. Producers are assumed to have the capability of accurately regulating their power output within a certain range. Power lines are assumed to be solid blocks of an electrically conductive material surrounded by a layer of insulating material. Their cross-section is assumed to be constant along the entire length of the power line. Since both heating and power loss increase with current but not with voltage, it is always preferable to transfer direct current at the highest possible voltage which is allowed by the design of the power line. Therefore, only the electrical current is considered as a control.
The power loss in a power line is given by 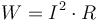 where
where 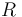 is the resistance of the power line which is derived from the resistivity of the conductor using the formula
is the resistance of the power line which is derived from the resistivity of the conductor using the formula
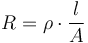
where 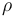 is the resistivity of the conductor,
is the resistivity of the conductor, 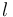 is the length of the conductor and
is the length of the conductor and 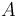 is the the cross-sectional area of the conducting material within the power line. Resistivity is assumed to vary exponentially with the temperature of the conducting material, meaning that
is the the cross-sectional area of the conducting material within the power line. Resistivity is assumed to vary exponentially with the temperature of the conducting material, meaning that 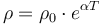 where
where 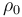 is the resistivity of the conducting material at room temperature (which is defined as
is the resistivity of the conducting material at room temperature (which is defined as 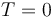 ) and
) and 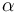 is a material-specific dimensionless constant. This causes a steady power loss of
is a material-specific dimensionless constant. This causes a steady power loss of
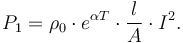
The lost energy is transformed into heat which raises the temperature of the conductor. As the conductor is now hotter than the air surrounding its layer of insulating material, heat is steadily lost at a rate determined by the temperature difference, the conductors surface area and the insulating material's heat conductivity. The heat loss is given by
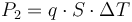
where 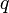 is the ratio between the isolating material's thermal conductivity and its thickness,
is the ratio between the isolating material's thermal conductivity and its thickness, 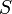 is the surface area of the power line and
is the surface area of the power line and 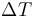 is the difference between the conductor's temperature and the surrounding air's temperature (which we will assume to be the same as room temperature, i.e.
is the difference between the conductor's temperature and the surrounding air's temperature (which we will assume to be the same as room temperature, i.e. 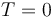 ). In summary, the rate at which the heat stored in a power line changes is given by
). In summary, the rate at which the heat stored in a power line changes is given by
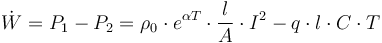
where 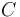 is the circumference of the cross-section of the power line. Assuming constant density, we can use the conducting materials volume-specific heat capacity which we will refer to as
is the circumference of the cross-section of the power line. Assuming constant density, we can use the conducting materials volume-specific heat capacity which we will refer to as 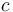 , we can calculate the change in temperature from the change in heat:
, we can calculate the change in temperature from the change in heat:
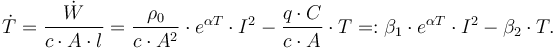
For the examples in this article, we will assume the conductor to be solid copper surrounded by a
Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex]
\mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\
& \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\
& \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex]
& x(0) &=& (0.5, 0.7, 0)^T, \\
& w(t) &\in& \{0, 1\}.
\end{array}](https://mintoc.de/images/math/1/0/1/101f9757fbe04ebd1e38721a62291665.png)
Here the differential states 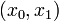 describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation
describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation 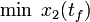 . The decision, whether the fishing fleet is actually fishing at time
. The decision, whether the fishing fleet is actually fishing at time  is denoted by
is denoted by 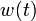 .
.
Parameters
These fixed values are used within the model.
![\begin{array}{rcl}
[t_0, t_f] &=& [0, 12],\\
(c_0, c_1) &=& (0.4, 0.2).
\end{array}](https://mintoc.de/images/math/c/0/d/c0d44a47d896216ce3c5ba02b67a90ff.png)
Reference Solutions
If the problem is relaxed, i.e., we demand that 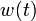 be in the continuous interval
be in the continuous interval ![[0, 1]](https://mintoc.de/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) instead of the binary choice
instead of the binary choice 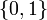 , the optimal solution can be determined by means of Pontryagins maximum principle. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.
, the optimal solution can be determined by means of Pontryagins maximum principle. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.
The optimal objective value of this relaxed problem is 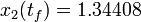 . As follows from MIOC theory<bibref>Sager2008</bibref> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of
. As follows from MIOC theory<bibref>Sager2008</bibref> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of 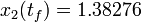 , and one with 56 switches and
, and one with 56 switches and 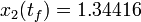 .
.
- Reference solution plots
Source Code
Model descriptions are available in
- AMPL code at Lotka Volterra fishing problem (AMPL)
- C code at Lotka Volterra fishing problem (C)
- optimica code at Lotka Volterra fishing problem (optimica)
- JuMP code at Lotka Volterra fishing problem (JuMP)
- Muscod code at Lotka Volterra fishing problem (Muscod)
- ACADO code at Lotka Volterra fishing problem (ACADO)
- VPLAN code at Lotka Volterra fishing problem (VPLAN)
- Casadi code at Lotka Volterra fishing problem (Casadi)
- GloOptCon code at Lotka Volterra fishing problem (GloOptCon)
- switch code at Lotka Volterra fishing problem (switch)
Variants
There are several alternative formulations and variants of the above problem, in particular
- a prescribed time grid for the control function <bibref>Sager2006</bibref>, see also Lotka Volterra fishing problem (AMPL),
- a time-optimal formulation to get into a steady-state <bibref>Sager2005</bibref>,
- the usage of a different target steady-state, as the one corresponding to
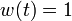 which is
which is 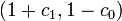 ,
, - different fishing control functions for the two species,
- different parameters and start values.
Miscellaneous and Further Reading
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bibref>Sager2006</bibref> and revisited in his PhD thesis <bibref>Sager2005</bibref>. These are also the references to look for more details.
References
<bibreferences/>



