Difference between revisions of "Lotka Volterra fishing problem"

From mintOC
Jump to: navigation, search
m (Text replacement - "<bibreferences/>" to "<biblist />")
m (Text replacement - "\<bibref\>(.*)\<\/bibref\>" to "<bib id="$1" />")
Line 48: Line 48:
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of [http://en.wikipedia.org/wiki/Pontryagin%27s_minimum_principle Pontryagins maximum principle]. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of [http://en.wikipedia.org/wiki/Pontryagin%27s_minimum_principle Pontryagins maximum principle]. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.
  
−
The optimal objective value of this relaxed problem is <math>x_2(t_f) = 1.34408</math>. As follows from MIOC theory<bibref>Sager2008</bibref> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of <math>x_2(t_f) = 1.38276</math>, and one with 56 switches and <math>x_2(t_f) = 1.34416</math>.
+
The optimal objective value of this relaxed problem is <math>x_2(t_f) = 1.34408</math>. As follows from MIOC theory<bib id="Sager2008" /> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of <math>x_2(t_f) = 1.38276</math>, and one with 56 switches and <math>x_2(t_f) = 1.34416</math>.
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
Line 76: Line 76:
 
There are several alternative formulations and variants of the above problem, in particular
 
There are several alternative formulations and variants of the above problem, in particular
  
−
* a prescribed time grid for the control function <bibref>Sager2006</bibref>, see also [[Lotka Volterra fishing problem (AMPL)]],
+
* a prescribed time grid for the control function <bib id="Sager2006" />, see also [[Lotka Volterra fishing problem (AMPL)]],
−
* a time-optimal formulation to get into a steady-state <bibref>Sager2005</bibref>,
+
* a time-optimal formulation to get into a steady-state <bib id="Sager2005" />,
 
* the usage of a different target steady-state, as the one corresponding to <math> w(t) = 1</math> which is <math>(1 + c_1, 1 - c_0)</math>,
 
* the usage of a different target steady-state, as the one corresponding to <math> w(t) = 1</math> which is <math>(1 + c_1, 1 - c_0)</math>,
 
* different fishing control functions for the two species,
 
* different fishing control functions for the two species,
Line 83: Line 83:
  
 
== Miscellaneous and Further Reading ==
 
== Miscellaneous and Further Reading ==
−
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bibref>Sager2006</bibref> and revisited in his PhD thesis <bibref>Sager2005</bibref>. These are also the references to look for more details.
+
The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bib id="Sager2006" /> and revisited in his PhD thesis <bib id="Sager2005" />. These are also the references to look for more details.
  
 
== References ==
 
== References ==

Revision as of 21:32, 30 December 2015

Lotka Volterra fishing problem
State dimension: 1
Differential states: 3
Discrete control functions: 1
Interior point equalities: 3


The Lotka Volterra fishing problem looks for an optimal fishing strategy to be performed on a fixed time horizon to bring the biomasses of both predator as prey fish to a prescribed steady state. The problem was set up as a small-scale benchmark problem. The well known Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man. The control can be regarded both in a relaxed, as in a discrete manner, corresponding to a part of the fleet, or the full fishing fleet.


The mathematical equations form a small-scale ODE model. The interior point equality conditions fix the initial values of the differential states.

The optimal integer control functions shows chattering behavior, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\ & \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex] & x(0) &=& (0.5, 0.7, 0)^T, \\ & w(t) &\in& \{0, 1\}. \end{array}

Here the differential states 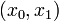(x_0, x_1) describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation 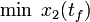\min \; x_2(t_f). The decision, whether the fishing fleet is actually fishing at time t is denoted by w(t).

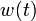Parameters

These fixed values are used within the model.

\begin{array}{rcl} [t_0, t_f] &=& [0, 12],\\ (c_0, c_1) &=& (0.4, 0.2). \end{array}

Reference Solutions

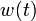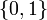If the problem is relaxed, i.e., we demand that w(t) be in the continuous interval [0, 1] instead of the binary choice \{0,1\}, the optimal solution can be determined by means of Pontryagins maximum principle. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.

The optimal objective value of this relaxed problem is 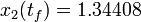x_2(t_f) = 1.34408. As follows from MIOC theory[Sager2008]The entry doesn't exist yet. this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. 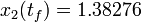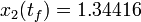As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of x_2(t_f) = 1.38276, and one with 56 switches and x_2(t_f) = 1.34416.

  • Reference solution plots

  • Optimal relaxed control determined by an indirect approach and by a direct approach on different control discretization grids.

  • Differential states and corresponding adjoint variables in the indirect approach.

  • Control and differential states with only two switches.

  • Control and differential states with 56 switches.


Source Code

Model descriptions are available in

Variants

There are several alternative formulations and variants of the above problem, in particular

  • a prescribed time grid for the control function [Sager2006]Address: Heidelberg
    Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
    Booktitle: Recent Advances in Optimization
    Editor: A. Seeger
    Note: ISBN 978-3-5402-8257-0
    Pages: 269--289
    Publisher: Springer
    Series: Lectures Notes in Economics and Mathematical Systems
    Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
    Volume: 563
    Year: 2009
    Link to Google Scholar    , see also Lotka Volterra fishing problem (AMPL),
  • a time-optimal formulation to get into a steady-state [Sager2005]Address: Tönning, Lübeck, Marburg
    Author: S. Sager
    Editor: ISBN 3-89959-416-9
    Publisher: Der andere Verlag
    Title: Numerical methods for mixed--integer optimal control problems
    Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
    Year: 2005
    Link to Google Scholar    ,
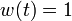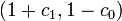  • the usage of a different target steady-state, as the one corresponding to w(t) = 1 which is (1 + c_1, 1 - c_0),
  • different fishing control functions for the two species,
  • different parameters and start values.

Miscellaneous and Further Reading

The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper [Sager2006]Address: Heidelberg
Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
Booktitle: Recent Advances in Optimization
Editor: A. Seeger
Note: ISBN 978-3-5402-8257-0
Pages: 269--289
Publisher: Springer
Series: Lectures Notes in Economics and Mathematical Systems
Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
Volume: 563
Year: 2009
Link to Google Scholar and revisited in his PhD thesis [Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005
Link to Google Scholar. These are also the references to look for more details.

References

[Sager2005]S. Sager (2005): Numerical methods for mixed--integer optimal control problems. (%edition%). Der andere Verlag, Tönning, Lübeck, Marburg, %pages%Link to Google Scholar
[Sager2006]S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder (2009): Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem. Springer, Recent Advances in OptimizationLink to Google Scholar
[Sager2008]The entry doesn't exist yet.
Retrieved from "https://mintoc.de/index.php?title=Lotka_Volterra_fishing_problem&oldid=1110"