Difference between revisions of "Category:Path-constrained arcs"
From mintOC
m (Initial setup of IMA paper text) |
(No difference)
|
Revision as of 13:26, 20 November 2010
Whenever a path constraint is active, i.e., it holds ![c_i(x(t)) = 0 \; \forall \; t \in [t^\text{start}, t^\text{end}] \subseteq [0, t_f]](https://mintoc.de/images/math/b/2/a/b2ae1f8d2da30f32c01f209278698096.png)
, and no continuous control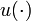 
can be determined to compensate for the changes in 
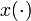, naturally 
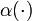needs to do so by taking values in the interior of its feasible domain. An illustrating example has been given in <bibref>Sager2009</bibref>, where velocity limitations for the energy-optimal operation of New York subway trains are taken into account. The optimal integer solution does only exist in the limit case of infinite switching (Zeno behavior), or when a tolerance is given.
References
<bibreferences/>
Pages in category "Path-constrained arcs"
The following 10 pages are in this category, out of 10 total.
