Difference between revisions of "Category:Bang bang"
From mintOC
m |
m |
||
| Line 1: | Line 1: | ||
| − | + | Bang-bang arcs are time intervals on which the control bounds are active, i.e., <math>\alpha_i(t) \in \{0,1\} \; \forall \; t</math>. The case where the optimal solution contains only bang-bang arcs is in a sense the easiest. The solution of the relaxed MIOCP will be integer feasible, if the control discretization grid is a superset of the switching points of the optimal control. Hence, the main goal will be to adapt the control discretization grid such that the solution of the relaxed problem is already integer. Also on fixed time grids good solutions are easy to come up with, as rounded solutions approximate the integrated difference between relaxed and binary solution very well. | |
[[Category:Solution characterization]] | [[Category:Solution characterization]] | ||
Latest revision as of 13:22, 20 November 2010
Bang-bang arcs are time intervals on which the control bounds are active, i.e.,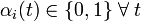 
. The case where the optimal solution contains only bang-bang arcs is in a sense the easiest. The solution of the relaxed MIOCP will be integer feasible, if the control discretization grid is a superset of the switching points of the optimal control. Hence, the main goal will be to adapt the control discretization grid such that the solution of the relaxed problem is already integer. Also on fixed time grids good solutions are easy to come up with, as rounded solutions approximate the integrated difference between relaxed and binary solution very well.
Pages in category "Bang bang"
The following 17 pages are in this category, out of 17 total.
