Egerstedt standard problem

Egerstedt standard problem
State dimension:	1
Differential states:	3
Discrete control functions:	3
Path constraints:	1
Interior point equalities:	3

The Egerstedt standard problemm is the problem is of an academic nature and was proposed by Egerestedt to highlight the features of an Hybrid System algorithm in 2006 [Egerstedt2006]Author: M. Egerstedt; Y. Wardi; H. Axelsson
Journal: IEEE Transactions on Automatic Control
Pages: 110--115
Title: Transition-time optimization for switched-mode dynamical systems
Volume: 51
Year: 2006
. It has been used since then in many MIOCP research studies (e.g. [Jung2013]Author: M. Jung; C. Kirches; S. Sager
Booktitle: Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschel
Editor: M. J\"unger and G. Reinelt
Pages: 387--417
Publisher: Springer Berlin Heidelberg
Title: On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control
Url: http://www.mathopt.de/PUBLICATIONS/Jung2013.pdf
Year: 2013
) for benchmarking of MIOCP algorithms.

Mathematical formulation

The mixed-integer optimal control problem after partial outer convexification is given by

$\begin{array}{llclr} \displaystyle \min_{x, \omega} & x_3(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = & -x_1\omega_1 + (x_1+x_2)\omega_2+(x_1-x_2)\omega_3, \\ & \dot{x}_2 & = & (x_1+2x_2)\omega_1+(x_1-2x_2)\omega_2+(x_1+x_2)\omega_3, \\ & \dot{x}_3 & = & x_1^2+x_2^2, \\[1.5ex] & x(0) &=& (0.5, 0.5, 0)^T, \\ & x_2(t) & \geq & 0.4, \\ & 1 &=& \sum\limits_{i=1}^3\omega_i(t), \\ & \omega(t) &\in& \{0, 1\}, \end{array}$ for $t \in [t_0, t_f]=[0,1]$.

Reference Solutions

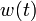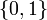If the problem is relaxed, i.e., we demand that $w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$, the optimal solution can be determined by means of Pontryagins maximum principle. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.

The optimal objective value of this relaxed problem is 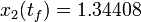$x_2(t_f) = 1.34408$. As follows from MIOC theory [Sager2011d]Author: S. Sager
How published: University of Heidelberg
Month: August
Note: Habilitation
Title: On the Integration of Optimization Approaches for Mixed-Integer Nonlinear Optimal Control
Url: http://mathopt.de/PUBLICATIONS/Sager2011d.pdf
Year: 2011
this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. 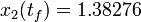As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of $x_2(t_f) = 1.38276$, and one with 56 switches and $x_2(t_f) = 1.34416$.

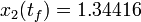• Reference solution plots
• 

  Optimal relaxed control determined by an indirect approach and by a direct approach on different control discretization grids.

• 

  Differential states and corresponding adjoint variables in the indirect approach.

• 

  Control and differential states with only two switches.

• 

  Control and differential states with 56 switches.

Source Code

Model descriptions are available in

• ACADO code at Lotka Volterra fishing problem (ACADO)
• AMPL code at Lotka Volterra fishing problem (AMPL)
• APMonitor code at Lotka Volterra fishing problem (APMonitor)
• Bocop code at Lotka Volterra fishing problem (Bocop)
• Casadi code at Lotka Volterra fishing problem (Casadi)
• JModelica code at Lotka Volterra fishing problem (JModelica)
• JuMP code at Lotka Volterra fishing problem (JuMP)
• Muscod code at Lotka Volterra fishing problem (Muscod)
• switch code at Lotka Volterra fishing problem (switch)
• PROPT code at Lotka Volterra fishing problem (TomDyn/PROPT)

Variants

There are several alternative formulations and variants of the above problem, in particular

• a prescribed time grid for the control function [Sager2006]Address: Heidelberg
  Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
  Booktitle: Recent Advances in Optimization
  Editor: A. Seeger
  Note: ISBN 978-3-5402-8257-0
  Pages: 269--289
  Publisher: Springer
  Series: Lectures Notes in Economics and Mathematical Systems
  Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
  Volume: 563
  Year: 2009
  , see also Lotka Volterra fishing problem (AMPL),
• a time-optimal formulation to get into a steady-state [Sager2005]Address: Tönning, Lübeck, Marburg
  Author: S. Sager
  Editor: ISBN 3-89959-416-9
  Publisher: Der andere Verlag
  Title: Numerical methods for mixed--integer optimal control problems
  Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
  Year: 2005
  ,
• the usage of a different target steady-state, as the one corresponding to 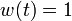$w(t) = 1$ which is 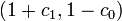$(1 + c_1, 1 - c_0)$, see Lotka Volterra multi-arcs problem
• different fishing control functions for the two species, see Lotka Volterra Multimode fishing problem
• different parameters and start values.

Miscellaneous and Further Reading

The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper [Sager2006]Address: Heidelberg
Author: S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder
Booktitle: Recent Advances in Optimization
Editor: A. Seeger
Note: ISBN 978-3-5402-8257-0
Pages: 269--289
Publisher: Springer
Series: Lectures Notes in Economics and Mathematical Systems
Title: Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem
Volume: 563
Year: 2009
and revisited in his PhD thesis [Sager2005]Address: Tönning, Lübeck, Marburg
Author: S. Sager
Editor: ISBN 3-89959-416-9
Publisher: Der andere Verlag
Title: Numerical methods for mixed--integer optimal control problems
Url: http://mathopt.de/PUBLICATIONS/Sager2005.pdf
Year: 2005
. These are also the references to look for more details.

References

[Egerstedt2006]	M. Egerstedt; Y. Wardi; H. Axelsson (2006): Transition-time optimization for switched-mode dynamical systems. IEEE Transactions on Automatic Control, 51, 110--115
[Jung2013]	M. Jung; C. Kirches; S. Sager (2013): On Perspective Functions and Vanishing Constraints in Mixed-Integer Nonlinear Optimal Control. Facets of Combinatorial Optimization -- Festschrift for Martin Gr\"otschel
[Sager2005]	S. Sager (2005): Numerical methods for mixed--integer optimal control problems. (%edition%). Der andere Verlag, Tönning, Lübeck, Marburg, %pages%
[Sager2006]	S. Sager; H.G. Bock; M. Diehl; G. Reinelt; J.P. Schl\"oder (2009): Numerical methods for optimal control with binary control functions applied to a Lotka-Volterra type fishing problem. Springer, Recent Advances in Optimization
[Sager2011d]	S. Sager: On the Integration of Optimization Approaches for Mixed-Integer Nonlinear Optimal Control, 2011

We present numerical results for a benchmark MIOCP from a previous study [157] with the addition of switching constraints. In its original form, the problem was:

After partial outer convexification with respect to the integer control v, the binary convexified counterpart problem reads