Difference between revisions of "Category:ODE model"
(Added mathematical problem definition) |
m (Added Outer convexification) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | This category includes all problems constrained by the solution of [http://en.wikipedia.org/wiki/Ordinary_differential_equation ordinary differential equations] (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable | + | This category includes all problems constrained by the solution of [http://en.wikipedia.org/wiki/Ordinary_differential_equation ordinary differential equations] (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only (typically time) are present in the [[:Category:Model characterization|model equations]] for <math>F(\cdot)</math>. |
The mixed-integer optimal control problem is of the form | The mixed-integer optimal control problem is of the form | ||
| Line 5: | Line 5: | ||
<math> | <math> | ||
\begin{array}{llcl} | \begin{array}{llcl} | ||
| − | \displaystyle \min_{x(\cdot), u(\cdot), v(\cdot)} & \phi(x(t_f)) \\[1.5ex] | + | \displaystyle \min_{x(\cdot), u(\cdot), v(\cdot), q, \rho} & \phi(x(t_f), q, \rho) \\[1.5ex] |
| − | \mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t)), \\ | + | \mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t), q, \rho), \\ |
| − | & 0 &\le& c(x(t),u(t),v(t)), \\[1.5ex] | + | & 0 &\le& c(x(t),u(t),v(t), q, \rho), \\[1.5ex] |
| − | & 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m)), \\ | + | & 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\ |
| − | & 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m)), \\ | + | & 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\[1.5ex] |
| − | & v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \} | + | & v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \},\\ |
| + | & \rho &\in& \Rho := \{\rho^1, \rho^2, \dots, \rho^{n_\Rho} \}, | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| − | + | for <math>t \in [t_0, t_f]</math> almost everywhere. | |
| − | The equality constraints <math>r^{\text{eq}}(\cdot)</math> will often fix the initial values, i.e., <math>x(0) = x_0</math>, or impose | + | <math>x(\cdot)</math> denotes the differential states, |
| + | <math>u(\cdot)</math> denotes the continuous control functions, | ||
| + | <math>v(\cdot)</math> denotes the integer control functions, | ||
| + | <math>q</math> denotes the continuous (constant-in-time) control values, | ||
| + | <math>\rho</math> denotes the integer (constant-in-time) control values. | ||
| + | |||
| + | The multipoint constraints <math>r^\cdot(\cdot)</math> are defined on a time grid <math>t_0 \le t_1 \le \dots \le t_m = t_f </math>. The Mayer term functional <math>\phi: \mathbb{R}^{n_x + n_q} \rightarrow \mathbb{R}</math>, the path- and control constraints <math>c: \mathbb{R}^{n_x \times n_u + n_v + n_q} \rightarrow \mathbb{R}^{n_c}</math> and the constraint functions <math>r^\cdot: \mathbb{R}^{(m+1) n_x + n_q} \rightarrow \mathbb{R}^{n_{r\cdot}}</math> are assumed to be sufficiently often differentiable. | ||
| + | |||
| + | The equality constraints <math>r^{\text{eq}}(\cdot)</math> will often fix the initial values, i.e., <math>x(0) = x_0</math>, or impose a [[:Category:Periodic | periodicity]] constraint. | ||
| + | |||
| + | == Extensions == | ||
| + | * For some problems the functions may as well depend explicitely on the time <math>t</math>. | ||
| + | * The differential equations might depend on [[:Category:State dependent switches | state-dependent switches]]. | ||
| + | * The variables may include [[:Category:Boolean variables | boolean variables]]. | ||
| + | * The underlying process might be a [[:Category:Multistage process | multistage process]]. | ||
| + | * The dynamics might be [[:Category:Unstable | unstable]]. | ||
| + | * There might be an underlying [[:Category:Network topology | network topology]]. | ||
| + | * The integer control functions might have been (re)formulated by means of an [[:Category:Outer convexification|outer convexification]]. | ||
| + | |||
| + | Note that a Lagrange term <math>\int_{t_0}^{t_f} L( x(t), u(t), v(t), q, \rho) \; \mathrm{d} t</math> can be transformed into a Mayer-type objective functional. | ||
[[Category:Model characterization]] | [[Category:Model characterization]] | ||
Latest revision as of 13:02, 20 November 2010
This category includes all problems constrained by the solution of ordinary differential equations (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only (typically time) are present in the model equations for 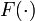 .
.
The mixed-integer optimal control problem is of the form
![\begin{array}{llcl}
\displaystyle \min_{x(\cdot), u(\cdot), v(\cdot), q, \rho} & \phi(x(t_f), q, \rho) \\[1.5ex]
\mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t), q, \rho), \\
& 0 &\le& c(x(t),u(t),v(t), q, \rho), \\[1.5ex]
& 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\
& 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\[1.5ex]
& v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \},\\
& \rho &\in& \Rho := \{\rho^1, \rho^2, \dots, \rho^{n_\Rho} \},
\end{array}](https://mintoc.de/images/math/c/2/e/c2ea6ba320c6ca71260f7eeb98105969.png)
for ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) almost everywhere.
almost everywhere.
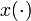 denotes the differential states,
denotes the differential states,
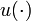 denotes the continuous control functions,
denotes the continuous control functions,
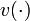 denotes the integer control functions,
denotes the integer control functions,
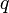 denotes the continuous (constant-in-time) control values,
denotes the continuous (constant-in-time) control values,
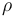 denotes the integer (constant-in-time) control values.
denotes the integer (constant-in-time) control values.
The multipoint constraints 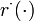 are defined on a time grid
are defined on a time grid 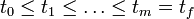 . The Mayer term functional
. The Mayer term functional 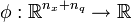 , the path- and control constraints
, the path- and control constraints 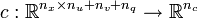 and the constraint functions
and the constraint functions 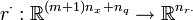 are assumed to be sufficiently often differentiable.
are assumed to be sufficiently often differentiable.
The equality constraints 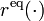 will often fix the initial values, i.e.,
will often fix the initial values, i.e., 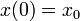 , or impose a periodicity constraint.
, or impose a periodicity constraint.
Extensions
- For some problems the functions may as well depend explicitely on the time
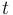 .
. - The differential equations might depend on state-dependent switches.
- The variables may include boolean variables.
- The underlying process might be a multistage process.
- The dynamics might be unstable.
- There might be an underlying network topology.
- The integer control functions might have been (re)formulated by means of an outer convexification.
Note that a Lagrange term 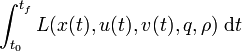 can be transformed into a Mayer-type objective functional.
can be transformed into a Mayer-type objective functional.
Pages in category "ODE model"
The following 52 pages are in this category, out of 52 total.