Difference between revisions of "Category:ODE model"
From mintOC
m (New page: This category includes all problems constrained by the solution of [http://en.wikipedia.org/wiki/Ordinary_differential_equation ordinary differential equations] (ODE). In particular, no al...) |
(Added mathematical problem definition) |
||
| Line 1: | Line 1: | ||
This category includes all problems constrained by the solution of [http://en.wikipedia.org/wiki/Ordinary_differential_equation ordinary differential equations] (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only are present in the mathematical model. | This category includes all problems constrained by the solution of [http://en.wikipedia.org/wiki/Ordinary_differential_equation ordinary differential equations] (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only are present in the mathematical model. | ||
| + | |||
| + | The mixed-integer optimal control problem is of the form | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{llcl} | ||
| + | \displaystyle \min_{x(\cdot), u(\cdot), v(\cdot)} & \phi(x(t_f)) \\[1.5ex] | ||
| + | \mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t)), \\ | ||
| + | & 0 &\le& c(x(t),u(t),v(t)), \\[1.5ex] | ||
| + | & 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m)), \\ | ||
| + | & 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m)), \\ | ||
| + | & v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \}. | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | The multipoint constraints <math>r^\cdot(\cdot)</math> are defined on a time grid <math>t_0 \le t_1 \le \dots \le t_m = t_f </math>. The Mayer term functional <math>\phi: \mathbb{R}^{n_x} \rightarrow \mathbb{R}</math>, the path- and control constraints <math>c: \mathbb{R}^{n_x \times n_u \times n_v} \rightarrow \mathbb{R}^{n_c}</math> and the constraint functions <math>r^\cdot: \mathbb{R}^{(m+1) n_x} \rightarrow \mathbb{R}^{n_{r\cdot}}</math> are assumed to be sufficiently often differentiable. | ||
| + | |||
| + | The equality constraints <math>r^{\text{eq}}(\cdot)</math> will often fix the initial values, i.e., <math>x(0) = x_0</math>, or impose of [[:Category:Periodic | periodicity]] constraint. | ||
[[Category:Model characterization]] | [[Category:Model characterization]] | ||
Revision as of 02:51, 29 November 2008
This category includes all problems constrained by the solution of ordinary differential equations (ODE). In particular, no algebraic variables and derivatives with respect to one independent variable only are present in the mathematical model.
The mixed-integer optimal control problem is of the form
![\begin{array}{llcl}
\displaystyle \min_{x(\cdot), u(\cdot), v(\cdot)} & \phi(x(t_f)) \\[1.5ex]
\mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t)), \\
& 0 &\le& c(x(t),u(t),v(t)), \\[1.5ex]
& 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m)), \\
& 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m)), \\
& v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \}.
\end{array}](https://mintoc.de/images/math/f/5/4/f54c92a1655a92f2209e7deb57343b9a.png)
The multipoint constraints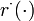 
are defined on a time grid 
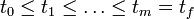. The Mayer term functional 
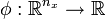, the path- and control constraints 
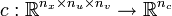and the constraint functions 
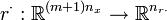are assumed to be sufficiently often differentiable.
The equality constraints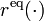 
will often fix the initial values, i.e., 
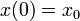, or impose of periodicity constraint.
Pages in category "ODE model"
The following 52 pages are in this category, out of 52 total.
